
AllQuestion and Answers: Page 1699
Question Number 39204 Answers: 0 Comments: 0
Question Number 39203 Answers: 0 Comments: 0
Question Number 39177 Answers: 2 Comments: 2
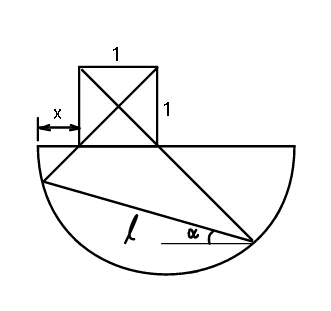
Question Number 39175 Answers: 1 Comments: 0
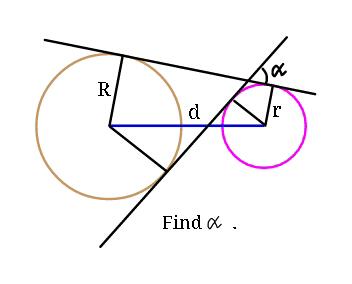
Question Number 39174 Answers: 1 Comments: 0

Question Number 39173 Answers: 0 Comments: 0
Question Number 39172 Answers: 1 Comments: 1
Question Number 39171 Answers: 1 Comments: 0
Question Number 39166 Answers: 1 Comments: 1
Question Number 39165 Answers: 0 Comments: 4
Question Number 39170 Answers: 0 Comments: 0
Question Number 39156 Answers: 1 Comments: 0

Question Number 39142 Answers: 1 Comments: 0
Question Number 39135 Answers: 1 Comments: 2
Question Number 39127 Answers: 0 Comments: 1
Question Number 39144 Answers: 1 Comments: 0
Question Number 39121 Answers: 0 Comments: 5
Question Number 39120 Answers: 1 Comments: 1
Question Number 39119 Answers: 0 Comments: 1
Question Number 39104 Answers: 1 Comments: 1

Question Number 39089 Answers: 2 Comments: 1
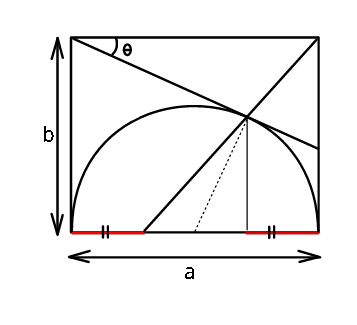
Question Number 39078 Answers: 1 Comments: 2
Question Number 39072 Answers: 2 Comments: 1

Question Number 39067 Answers: 2 Comments: 7

Question Number 39059 Answers: 1 Comments: 0
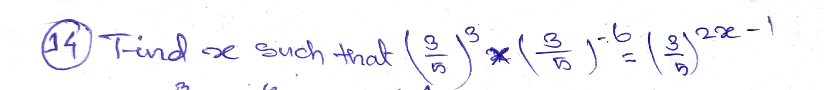
Question Number 39058 Answers: 1 Comments: 1
Pg 1694 Pg 1695 Pg 1696 Pg 1697 Pg 1698 Pg 1699 Pg 1700 Pg 1701 Pg 1702 Pg 1703
