Question and Answers Forum

All Questions Topic List

AllQuestion and Answers: Page 1689

Question Number 34283 Answers: 0 Comments: 2

calculate ∫_0 ^(π/2) (dx/(cos^4 x +sin^4 x))

$${calculate}\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\:\:\:\frac{{dx}}{{cos}^{\mathrm{4}} {x}\:+{sin}^{\mathrm{4}} {x}} \\ $$

Question Number 34282 Answers: 0 Comments: 1

find ∫_(π/6) ^(π/3) (dx/(cos(x) sin(x)))

$${find}\:\:\int_{\frac{\pi}{\mathrm{6}}} ^{\frac{\pi}{\mathrm{3}}} \:\:\:\:\:\:\frac{{dx}}{{cos}\left({x}\right)\:{sin}\left({x}\right)} \\ $$

Question Number 34281 Answers: 0 Comments: 0

calculate ∫_1 ^(√3) ((x−1)/(x^2 (x^2 +1)))dx

$${calculate}\:\:\:\int_{\mathrm{1}} ^{\sqrt{\mathrm{3}}} \:\:\:\:\:\:\frac{{x}−\mathrm{1}}{{x}^{\mathrm{2}} \left({x}^{\mathrm{2}} +\mathrm{1}\right)}{dx}\: \\ $$

Question Number 34280 Answers: 0 Comments: 0

find ∫ ((ln(x+x^2 ))/x^2 )dx

$${find}\:\:\:\:\int\:\:\:\frac{{ln}\left({x}+{x}^{\mathrm{2}} \right)}{{x}^{\mathrm{2}} }{dx} \\ $$

Question Number 34279 Answers: 0 Comments: 0

find ∫_1 ^(+∞) (((−1)^([x]) )/x) dx .

$${find}\:\:\int_{\mathrm{1}} ^{+\infty} \:\:\frac{\left(−\mathrm{1}\right)^{\left[{x}\right]} }{{x}}\:{dx}\:. \\ $$

Question Number 34278 Answers: 0 Comments: 0

find the value of ∫_0 ^∞ (2 +(t+3)ln(((t+2)/(t+4))))dt .

$${find}\:{the}\:{value}\:{of}\:\:\int_{\mathrm{0}} ^{\infty} \:\left(\mathrm{2}\:\:+\left({t}+\mathrm{3}\right){ln}\left(\frac{{t}+\mathrm{2}}{{t}+\mathrm{4}}\right)\right){dt}\:. \\ $$

Question Number 34277 Answers: 0 Comments: 1

calculate A_n =∫_0 ^∞ (dx/((x+1)(x+2)....(x+n))) n integr≥2 .

$${calculate}\:{A}_{{n}} =\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\frac{{dx}}{\left({x}+\mathrm{1}\right)\left({x}+\mathrm{2}\right)....\left({x}+{n}\right)} \\ $$$${n}\:{integr}\geqslant\mathrm{2}\:. \\ $$

Question Number 34276 Answers: 0 Comments: 0

nature of ∫_0 ^∞ (dx/(1+x^3 sin^2 x)) ?

$${nature}\:{of}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{3}} {sin}^{\mathrm{2}} {x}}\:? \\ $$

Question Number 34275 Answers: 0 Comments: 0

nature of ∫_0 ^∞ cos(e^x )dx?

$${nature}\:{of}\:\int_{\mathrm{0}} ^{\infty} \:{cos}\left({e}^{{x}} \right){dx}? \\ $$

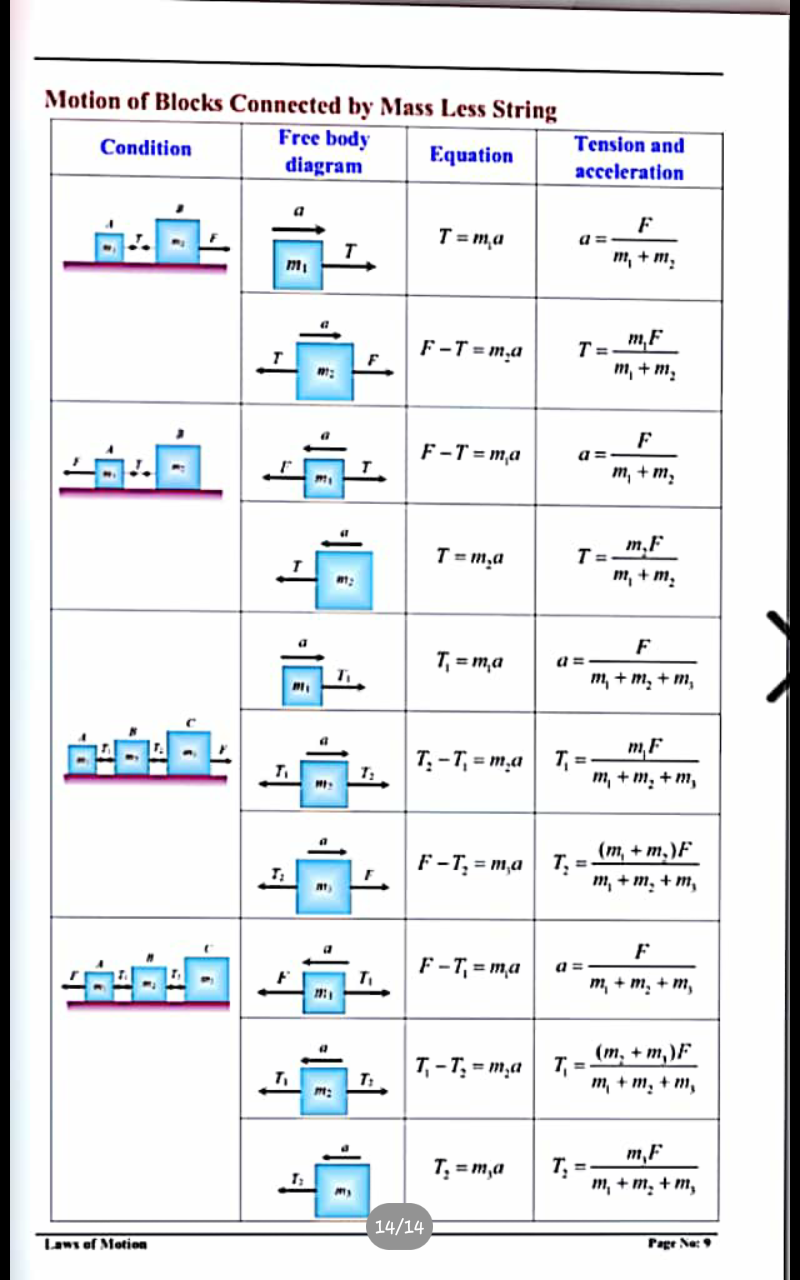
Question Number 34274 Answers: 0 Comments: 0

calculate ∫_2 ^(+∞) ((4x)/(x^4 −1))dx .

$${calculate}\:\:\int_{\mathrm{2}} ^{+\infty} \:\:\frac{\mathrm{4}{x}}{{x}^{\mathrm{4}} −\mathrm{1}}{dx}\:. \\ $$

Question Number 34273 Answers: 0 Comments: 0

calculate ∫_0 ^∞ (e^(arctanx) /(1+x^2 ))dx .

$${calculate}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\frac{{e}^{{arctanx}} }{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\:. \\ $$

Question Number 34271 Answers: 0 Comments: 0

find lim_(n→+∞) ∫_0 ^∞ ((arctan(nx))/(n(1+x^2 )))dx

$${find}\:{lim}_{{n}\rightarrow+\infty} \:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{arctan}\left({nx}\right)}{{n}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{dx} \\ $$

Question Number 34270 Answers: 0 Comments: 0

let give A_n = ∫_0 ^∞ (dx/((1+x^3 )^n )) 1) calculate A_1 2) for n≥2 find a relation between A_(n+1) and A_n 3) find the value of A_n .

$${let}\:{give}\:{A}_{{n}} =\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{{dx}}{\left(\mathrm{1}+{x}^{\mathrm{3}} \right)^{{n}} } \\ $$$$\left.\mathrm{1}\right)\:{calculate}\:{A}_{\mathrm{1}} \\ $$$$\left.\mathrm{2}\right)\:{for}\:{n}\geqslant\mathrm{2}\:{find}\:{a}\:{relation}\:{between}\:{A}_{{n}+\mathrm{1}} \:{and}\:{A}_{{n}} \\ $$$$\left.\mathrm{3}\right)\:{find}\:{the}\:{value}\:{of}\:{A}_{{n}} . \\ $$

Question Number 34269 Answers: 0 Comments: 0

calculate I(λ) =∫_0 ^∞ (dx/((1+x^2 )(1+x^λ )))

$${calculate}\:{I}\left(\lambda\right)\:=\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\:\frac{{dx}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\left(\mathrm{1}+{x}^{\lambda} \right)} \\ $$

Question Number 34268 Answers: 0 Comments: 0

calculate I = ∫_(−(π/2)) ^(π/2) ln(1+sinx)dx

$${calculate}\:{I}\:=\:\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left(\mathrm{1}+{sinx}\right){dx} \\ $$

Question Number 34267 Answers: 0 Comments: 1

calculate ∫_0 ^(+∞) (dx/((1+e^x )(1+e^(−x) ))) .

$${calculate}\:\:\int_{\mathrm{0}} ^{+\infty} \:\:\:\:\frac{{dx}}{\left(\mathrm{1}+{e}^{{x}} \right)\left(\mathrm{1}+{e}^{−{x}} \right)}\:. \\ $$

Question Number 34266 Answers: 0 Comments: 0

1) find the relation between ∫_x ^(+∞) e^(−t^2 ) dt and ∫_x ^(+∞) (e^(−t^2 ) /t^2 )dt 2) guive a equivalent to ∫_x ^(+∞) e^(−t^2 ) dt when x→+∞

$$\left.\mathrm{1}\right)\:{find}\:{the}\:{relation}\:{between}\:\int_{{x}} ^{+\infty} \:{e}^{−{t}^{\mathrm{2}} } {dt}\:\:{and} \\ $$$$\int_{{x}} ^{+\infty} \:\:\:\frac{{e}^{−{t}^{\mathrm{2}} } }{{t}^{\mathrm{2}} }{dt} \\ $$$$\left.\mathrm{2}\right)\:{guive}\:{a}\:{equivalent}\:{to}\:\int_{{x}} ^{+\infty} \:{e}^{−{t}^{\mathrm{2}} } {dt}\:{when}\:{x}\rightarrow+\infty \\ $$

Question Number 34265 Answers: 0 Comments: 0

find the value of ∫_0 ^∞ e^(−2t) sin([t]) dt .

$${find}\:{the}\:{value}\:{of}\:\:\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−\mathrm{2}{t}} \:{sin}\left(\left[{t}\right]\right)\:{dt}\:\:. \\ $$

Question Number 34264 Answers: 0 Comments: 0

find the value of ∫_0 ^∞ e^(−2[t]) sint dt

$${find}\:{the}\:{value}\:{of}\:\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−\mathrm{2}\left[{t}\right]} {sint}\:{dt} \\ $$

Question Number 34263 Answers: 0 Comments: 0

calculate I =∫_0 ^∞ (dx/((1+x^2 )(1+x^n ))) and J = ∫_0 ^∞ (x^n /((1+x^2 )(1+x^n )))dx with n integr >0

$${calculate}\:{I}\:\:=\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\frac{{dx}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\left(\mathrm{1}+{x}^{{n}} \right)}\:\:{and} \\ $$$${J}\:=\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\:\frac{{x}^{{n}} }{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\left(\mathrm{1}+{x}^{{n}} \right)}{dx}\:{with}\:{n}\:{integr}\:>\mathrm{0} \\ $$

Question Number 34262 Answers: 0 Comments: 0

find the nature of ∫_2 ^(+∞) ((√(1+t^2 +t^4 )) −t ^3 (√(t^3 +at)))dt a∈R .

$${find}\:{the}\:{nature}\:{of}\:\int_{\mathrm{2}} ^{+\infty} \left(\sqrt{\mathrm{1}+{t}^{\mathrm{2}} +{t}^{\mathrm{4}} \:}\:\:−{t}\:\:^{\mathrm{3}} \sqrt{{t}^{\mathrm{3}} +{at}}\right){dt} \\ $$$${a}\in{R}\:. \\ $$

Question Number 34261 Answers: 0 Comments: 0

study the convergence of ∫_0 ^∞ ((t−sint)/t^a )dt with a real.

$${study}\:{the}\:{convergence}\:{of}\:\:\int_{\mathrm{0}} ^{\infty} \:\frac{{t}−{sint}}{{t}^{{a}} }{dt}\:{with}\:{a}\:{real}. \\ $$

Question Number 34260 Answers: 0 Comments: 0

let give a>0 1) find the value of F(a) = ∫_0 ^∞ ((lnt)/(t^2 +a^2 ))dt 2) find the value of G(a)=∫_0 ^∞ ((aln(t))/((t^2 +a^2 )^2 ))dt 3) find the value of ∫_0 ^∞ ((ln(t))/((t^2 +3)^2 ))dt

$${let}\:{give}\:{a}>\mathrm{0} \\ $$$$\left.\mathrm{1}\right)\:{find}\:{the}\:{value}\:{of}\:\:{F}\left({a}\right)\:=\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{lnt}}{{t}^{\mathrm{2}} \:+{a}^{\mathrm{2}} }{dt} \\ $$$$\left.\mathrm{2}\right)\:{find}\:{the}\:{value}\:{of}\:{G}\left({a}\right)=\int_{\mathrm{0}} ^{\infty} \:\frac{{aln}\left({t}\right)}{\left({t}^{\mathrm{2}} \:+{a}^{\mathrm{2}} \right)^{\mathrm{2}} }{dt} \\ $$$$\left.\mathrm{3}\right)\:{find}\:{the}\:{value}\:{of}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{ln}\left({t}\right)}{\left({t}^{\mathrm{2}} \:+\mathrm{3}\right)^{\mathrm{2}} }{dt} \\ $$

Question Number 34258 Answers: 0 Comments: 1

1) prove that ∀ x∈]0,1[ 1−(1/x)≤lnx≤ x−1 2) find 2 sequences u_n and v_n / u_n ≤Π_(k=1) ^(n−1) ln((k/n))≤v_n ∀n≥2

$$\left.\mathrm{1}\left.\right)\:{prove}\:{that}\:\forall\:{x}\in\right]\mathrm{0},\mathrm{1}\left[\:\:\mathrm{1}−\frac{\mathrm{1}}{{x}}\leqslant{lnx}\leqslant\:{x}−\mathrm{1}\right. \\ $$$$\left.\mathrm{2}\right)\:{find}\:\mathrm{2}\:{sequences}\:{u}_{{n}} \:{and}\:{v}_{{n}} \:\:\:/ \\ $$$${u}_{{n}} \leqslant\prod_{{k}=\mathrm{1}} ^{{n}−\mathrm{1}} \:{ln}\left(\frac{{k}}{{n}}\right)\leqslant{v}_{{n}} \:\:\:\:\forall{n}\geqslant\mathrm{2} \\ $$

Question Number 34257 Answers: 0 Comments: 0

find f(x)= ∫_1 ^x (dt/(t(√(1+t^2 )))) 2) calculate I =∫_1 ^(+∞) (dt/(t(√(1+t^2 ))))

$${find}\:{f}\left({x}\right)=\:\int_{\mathrm{1}} ^{{x}} \:\:\:\:\frac{{dt}}{{t}\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }} \\ $$$$\left.\mathrm{2}\right)\:{calculate}\:{I}\:=\int_{\mathrm{1}} ^{+\infty} \:\:\:\:\frac{{dt}}{{t}\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }} \\ $$

Question Number 34255 Answers: 0 Comments: 0

find g(x)= ∫_0 ^∞ ((ln(1+xt^2 ))/t^2 ) dt 2) calculate ∫_0 ^∞ ((ln(1+3t^2 ))/t^2 )dt .

$${find}\:\:{g}\left({x}\right)=\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{ln}\left(\mathrm{1}+{xt}^{\mathrm{2}} \right)}{{t}^{\mathrm{2}} }\:{dt} \\ $$$$\left.\mathrm{2}\right)\:{calculate}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{ln}\left(\mathrm{1}+\mathrm{3}{t}^{\mathrm{2}} \right)}{{t}^{\mathrm{2}} }{dt}\:. \\ $$

Pg 1684 Pg 1685 Pg 1686 Pg 1687 Pg 1688 Pg 1689 Pg 1690 Pg 1691 Pg 1692 Pg 1693

Terms of Service

Contact: info@tinkutara.com