
AllQuestion and Answers: Page 1688
Question Number 40008 Answers: 1 Comments: 1
Question Number 40007 Answers: 0 Comments: 1
Question Number 39995 Answers: 2 Comments: 0
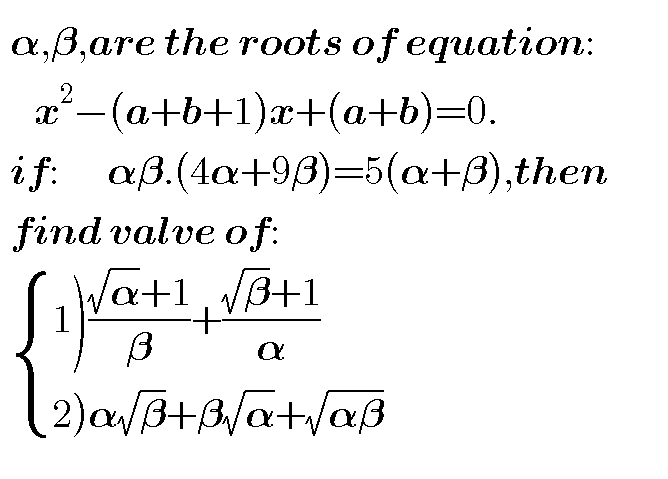
Question Number 39993 Answers: 2 Comments: 0
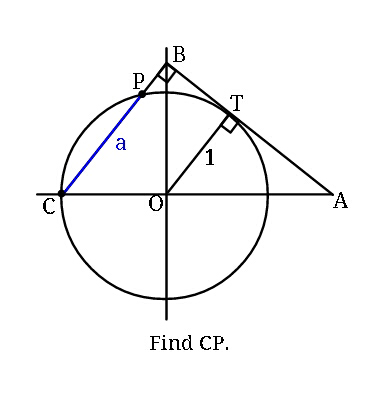
Question Number 39985 Answers: 1 Comments: 0

Question Number 39983 Answers: 1 Comments: 0
Question Number 39975 Answers: 0 Comments: 4
Question Number 39971 Answers: 3 Comments: 0
Question Number 39970 Answers: 1 Comments: 0

Question Number 39955 Answers: 1 Comments: 2

Question Number 39967 Answers: 0 Comments: 4
Question Number 39929 Answers: 1 Comments: 0

Question Number 39928 Answers: 0 Comments: 1
Question Number 39921 Answers: 4 Comments: 0

Question Number 39930 Answers: 1 Comments: 0

Question Number 39899 Answers: 0 Comments: 0
Question Number 39914 Answers: 0 Comments: 1

Question Number 39892 Answers: 0 Comments: 5
Question Number 39891 Answers: 0 Comments: 5
Question Number 39879 Answers: 2 Comments: 0
Question Number 39868 Answers: 2 Comments: 0
Question Number 39860 Answers: 1 Comments: 1

Question Number 39854 Answers: 2 Comments: 2
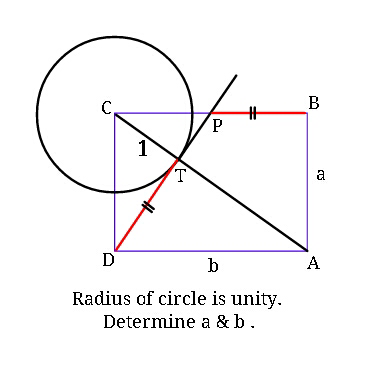
Question Number 39851 Answers: 2 Comments: 1

Question Number 39848 Answers: 2 Comments: 0

Question Number 39846 Answers: 2 Comments: 2
Pg 1683 Pg 1684 Pg 1685 Pg 1686 Pg 1687 Pg 1688 Pg 1689 Pg 1690 Pg 1691 Pg 1692
