
AllQuestion and Answers: Page 1687
Question Number 40283 Answers: 0 Comments: 0
Question Number 40277 Answers: 2 Comments: 0

Question Number 40276 Answers: 2 Comments: 0

Question Number 40271 Answers: 1 Comments: 0
Question Number 40270 Answers: 1 Comments: 0
Question Number 40260 Answers: 0 Comments: 2
Question Number 40251 Answers: 1 Comments: 0
Question Number 40255 Answers: 1 Comments: 2

Question Number 40254 Answers: 0 Comments: 3
Question Number 40238 Answers: 2 Comments: 0

Question Number 40237 Answers: 1 Comments: 4
Question Number 40236 Answers: 1 Comments: 0
Question Number 40231 Answers: 1 Comments: 0

Question Number 40222 Answers: 1 Comments: 0
Question Number 40218 Answers: 2 Comments: 0
Question Number 40216 Answers: 1 Comments: 0

Question Number 40213 Answers: 0 Comments: 0
Question Number 40212 Answers: 2 Comments: 1
$${Solve}\:\mathrm{4}{x}^{\mathrm{2}} −\mathrm{8}{x}−\mathrm{3}=\mathrm{0} \\ $$
Question Number 40188 Answers: 0 Comments: 0
$${can}\:{any}\:{one}\:{plss}\:{answer} \\ $$$${question}\:;\:\mathrm{40057} \\ $$
Question Number 40186 Answers: 0 Comments: 0

Question Number 40185 Answers: 0 Comments: 0

Question Number 40176 Answers: 0 Comments: 0

Question Number 40173 Answers: 1 Comments: 1
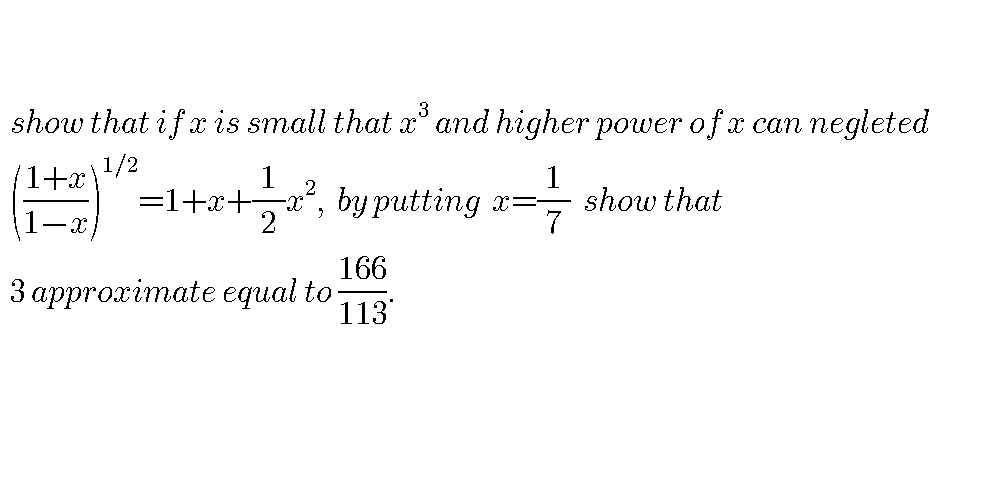
Question Number 40945 Answers: 0 Comments: 0
Question Number 40170 Answers: 1 Comments: 3
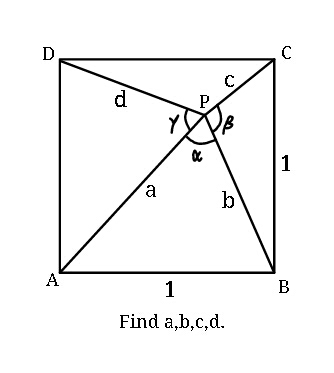
Question Number 40161 Answers: 0 Comments: 0
Pg 1682 Pg 1683 Pg 1684 Pg 1685 Pg 1686 Pg 1687 Pg 1688 Pg 1689 Pg 1690 Pg 1691
