
AllQuestion and Answers: Page 1686
Question Number 40457 Answers: 1 Comments: 0

Question Number 40442 Answers: 2 Comments: 0
Question Number 40434 Answers: 0 Comments: 3
$${prove}\:{that}\:\mathrm{ln}\left({x}\right)\:{is}\:{irrational}\:{for}\:{x}\:{natural} \\ $$
Question Number 40426 Answers: 0 Comments: 0

Question Number 40422 Answers: 1 Comments: 1
$$\mathrm{Solve}: \\ $$$$\mathrm{yd}{x}\:−\:{xdy}\:+\mathrm{log}\:{xdx}\:=\mathrm{0} \\ $$
Question Number 40418 Answers: 2 Comments: 1

Question Number 40417 Answers: 0 Comments: 0
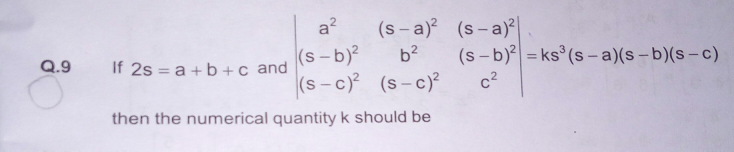
Question Number 40407 Answers: 1 Comments: 0
Question Number 40406 Answers: 1 Comments: 0

Question Number 40399 Answers: 3 Comments: 0
Question Number 40397 Answers: 1 Comments: 0
Question Number 40396 Answers: 0 Comments: 1
Question Number 40388 Answers: 1 Comments: 0

Question Number 40378 Answers: 1 Comments: 3
Question Number 40376 Answers: 0 Comments: 3
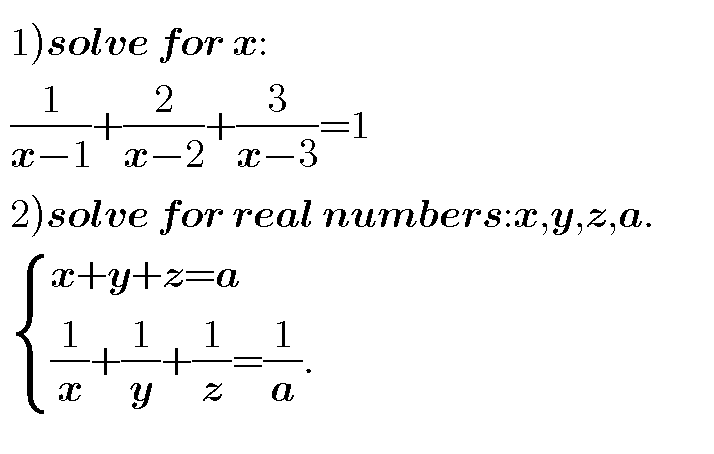
Question Number 40375 Answers: 1 Comments: 0

Question Number 40380 Answers: 2 Comments: 1
$${S}\mathrm{olve}\::\:\:\:\:\:\frac{\mathrm{dy}}{\mathrm{d}{x}}\:=\:\frac{{x}+{y}}{{x}−{y}} \\ $$
Question Number 40370 Answers: 0 Comments: 1
Question Number 40466 Answers: 1 Comments: 5
Question Number 40366 Answers: 0 Comments: 1
Question Number 40355 Answers: 1 Comments: 0

Question Number 40352 Answers: 0 Comments: 1
Question Number 40467 Answers: 1 Comments: 2
$$\int\mathrm{ln}\:\mid\sqrt{{x}+\mathrm{1}}+\sqrt{{x}}\mid\:{dx}= \\ $$
Question Number 40344 Answers: 1 Comments: 2
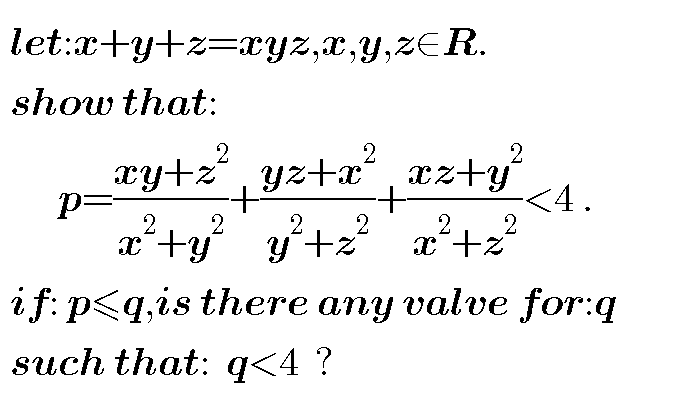
Question Number 40322 Answers: 1 Comments: 4
Question Number 40321 Answers: 0 Comments: 1
Pg 1681 Pg 1682 Pg 1683 Pg 1684 Pg 1685 Pg 1686 Pg 1687 Pg 1688 Pg 1689 Pg 1690
