
AllQuestion and Answers: Page 1682
Question Number 40892 Answers: 0 Comments: 0
Question Number 40891 Answers: 0 Comments: 1
Question Number 40890 Answers: 0 Comments: 2
Question Number 40889 Answers: 1 Comments: 0
Question Number 40888 Answers: 0 Comments: 0
Question Number 40887 Answers: 0 Comments: 1
Question Number 40886 Answers: 0 Comments: 0
Question Number 40885 Answers: 0 Comments: 1
Question Number 40884 Answers: 2 Comments: 0
Question Number 40883 Answers: 1 Comments: 0
Question Number 40882 Answers: 0 Comments: 0
Question Number 40880 Answers: 0 Comments: 0
Question Number 40878 Answers: 0 Comments: 0
Question Number 40876 Answers: 0 Comments: 0
Question Number 40875 Answers: 1 Comments: 0
Question Number 40874 Answers: 0 Comments: 0

Question Number 40873 Answers: 1 Comments: 0
Question Number 40872 Answers: 1 Comments: 2
Question Number 40870 Answers: 1 Comments: 1
Question Number 40868 Answers: 0 Comments: 4
$${calculate}\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{{x}}{{sinx}}{dx}\:\:. \\ $$
Question Number 40867 Answers: 0 Comments: 1
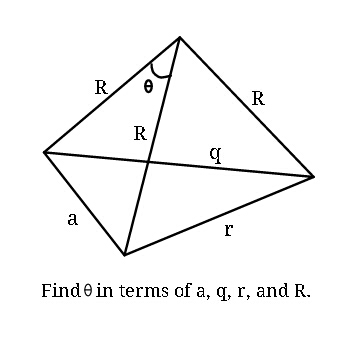
Question Number 40857 Answers: 1 Comments: 2

Question Number 40847 Answers: 1 Comments: 0
Question Number 40830 Answers: 0 Comments: 1
$${find}\:\int\:\sqrt{\mathrm{2}+{tan}^{\mathrm{2}} {t}}{dt} \\ $$
Question Number 40829 Answers: 1 Comments: 0
Question Number 40826 Answers: 1 Comments: 0
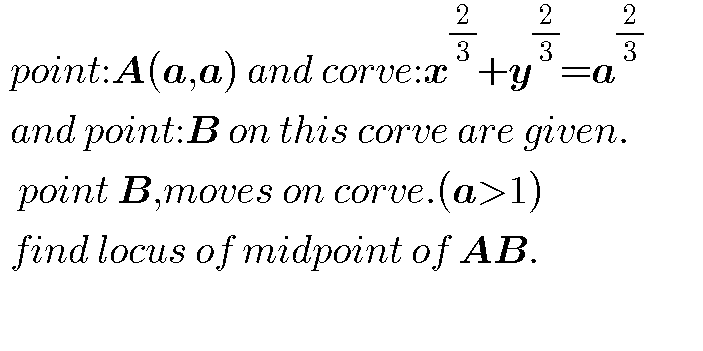
Pg 1677 Pg 1678 Pg 1679 Pg 1680 Pg 1681 Pg 1682 Pg 1683 Pg 1684 Pg 1685 Pg 1686
