
AllQuestion and Answers: Page 1680
Question Number 41095 Answers: 1 Comments: 0
Question Number 41086 Answers: 1 Comments: 0
Question Number 41084 Answers: 1 Comments: 0
$$\int\:\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{x}^{\mathrm{6}} \:+\:\mathrm{1}}\:\mathrm{dx} \\ $$
Question Number 41079 Answers: 1 Comments: 0
Question Number 41078 Answers: 1 Comments: 3
Question Number 41066 Answers: 1 Comments: 0

Question Number 41063 Answers: 0 Comments: 1

Question Number 41062 Answers: 0 Comments: 3
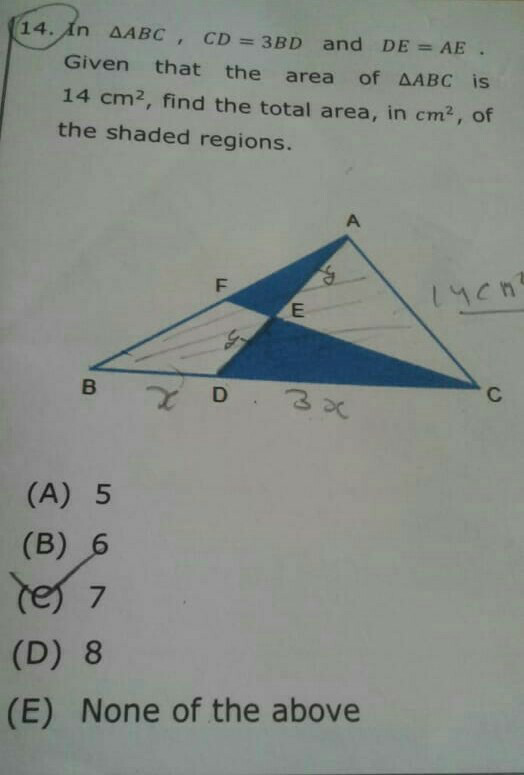
Question Number 41054 Answers: 0 Comments: 1
Question Number 41053 Answers: 4 Comments: 1
Question Number 41052 Answers: 0 Comments: 1
Question Number 41051 Answers: 0 Comments: 1
Question Number 41049 Answers: 0 Comments: 2
Question Number 41044 Answers: 1 Comments: 0

Question Number 41038 Answers: 1 Comments: 5

Question Number 41032 Answers: 1 Comments: 0
$$\frac{{a}}{{x}−{a}}\:+\frac{{b}}{{x}−{b}}=\mathrm{2}.{find}\:{x}. \\ $$
Question Number 41027 Answers: 1 Comments: 0
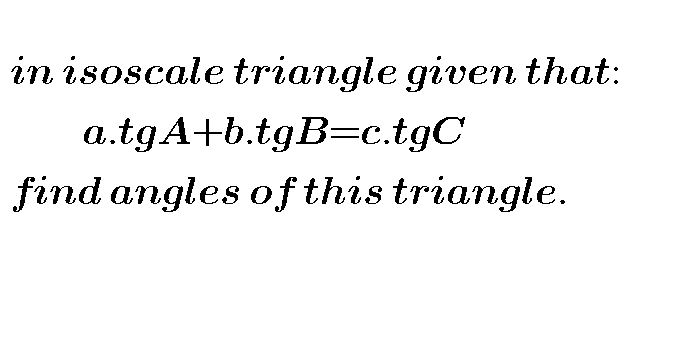
Question Number 41026 Answers: 1 Comments: 0

Question Number 41023 Answers: 0 Comments: 1

Question Number 47179 Answers: 1 Comments: 0

Question Number 47182 Answers: 0 Comments: 3
$${calculate}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{e}^{−{x}} \sqrt{\mathrm{1}−\sqrt{{x}}}{dx}\: \\ $$
Question Number 41016 Answers: 1 Comments: 1
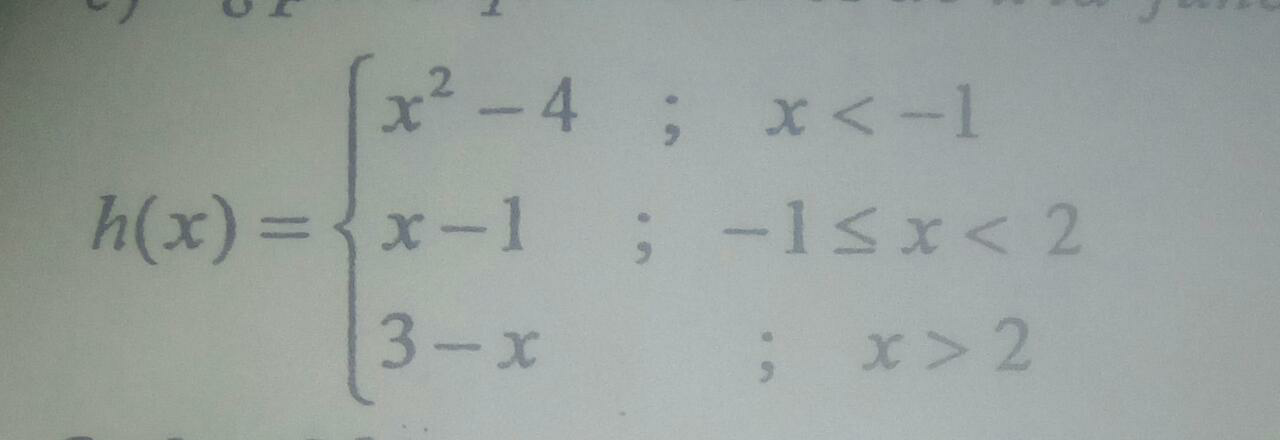
Question Number 41028 Answers: 1 Comments: 0
Question Number 41009 Answers: 1 Comments: 1

Question Number 41003 Answers: 2 Comments: 0
Question Number 40984 Answers: 0 Comments: 1
Pg 1675 Pg 1676 Pg 1677 Pg 1678 Pg 1679 Pg 1680 Pg 1681 Pg 1682 Pg 1683 Pg 1684
