
AllQuestion and Answers: Page 1679
Question Number 40817 Answers: 1 Comments: 0
Question Number 40816 Answers: 0 Comments: 0
Question Number 40815 Answers: 1 Comments: 0
Question Number 40814 Answers: 0 Comments: 3

Question Number 40813 Answers: 0 Comments: 4

Question Number 40804 Answers: 0 Comments: 6

Question Number 40787 Answers: 1 Comments: 4
Question Number 40786 Answers: 1 Comments: 0
Question Number 40782 Answers: 0 Comments: 0
Question Number 40773 Answers: 1 Comments: 0
Question Number 40771 Answers: 2 Comments: 1
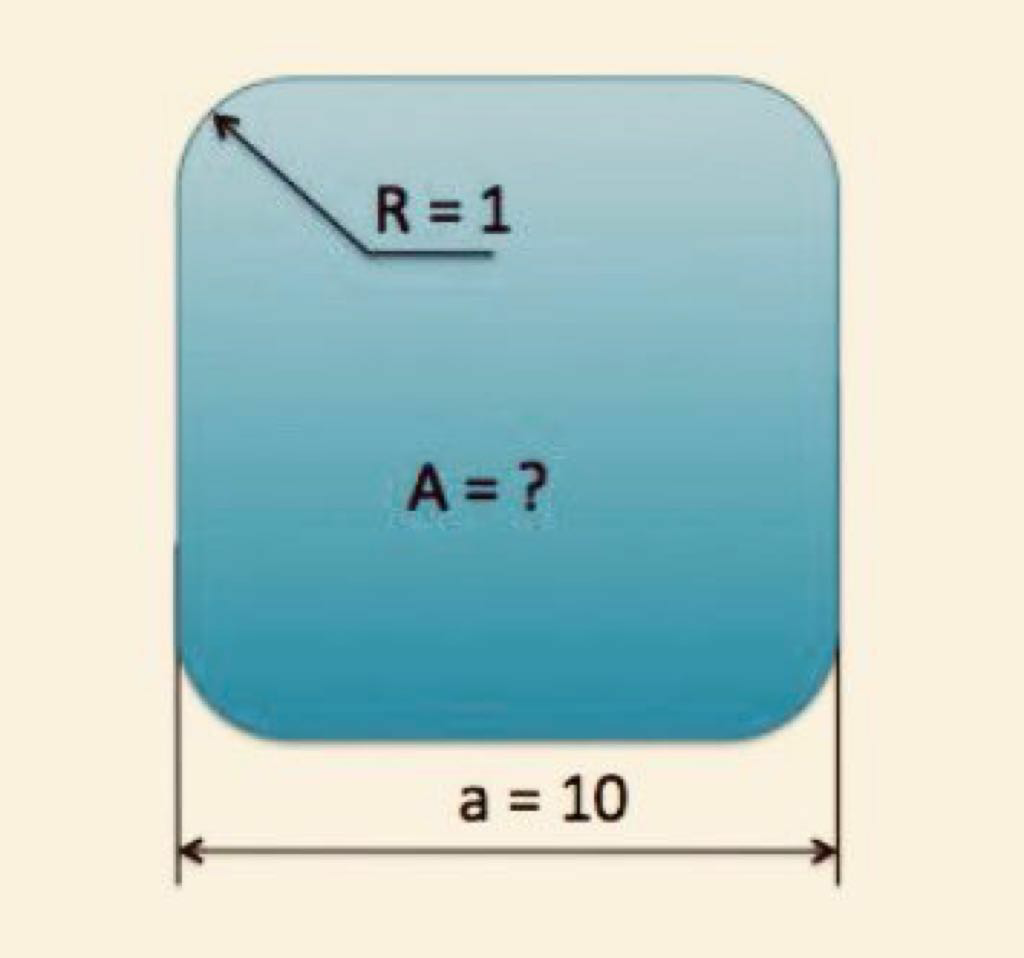
Question Number 40770 Answers: 1 Comments: 0
Question Number 40764 Answers: 1 Comments: 0
Question Number 40763 Answers: 2 Comments: 0

Question Number 40760 Answers: 0 Comments: 0
Question Number 40759 Answers: 1 Comments: 2
Question Number 40745 Answers: 3 Comments: 0
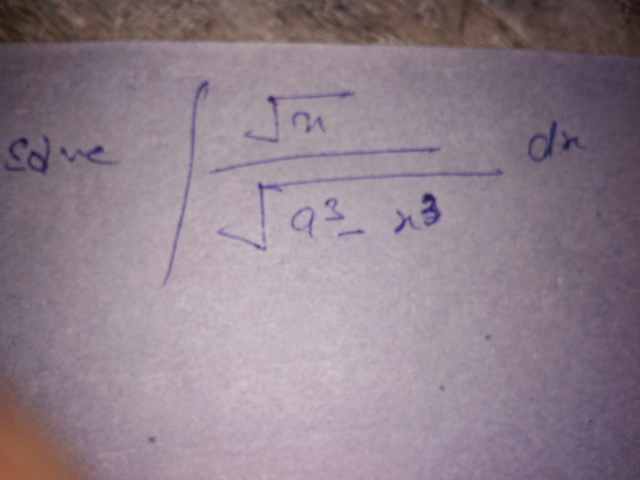
Question Number 40743 Answers: 2 Comments: 0

Question Number 40740 Answers: 0 Comments: 5

Question Number 40738 Answers: 2 Comments: 2
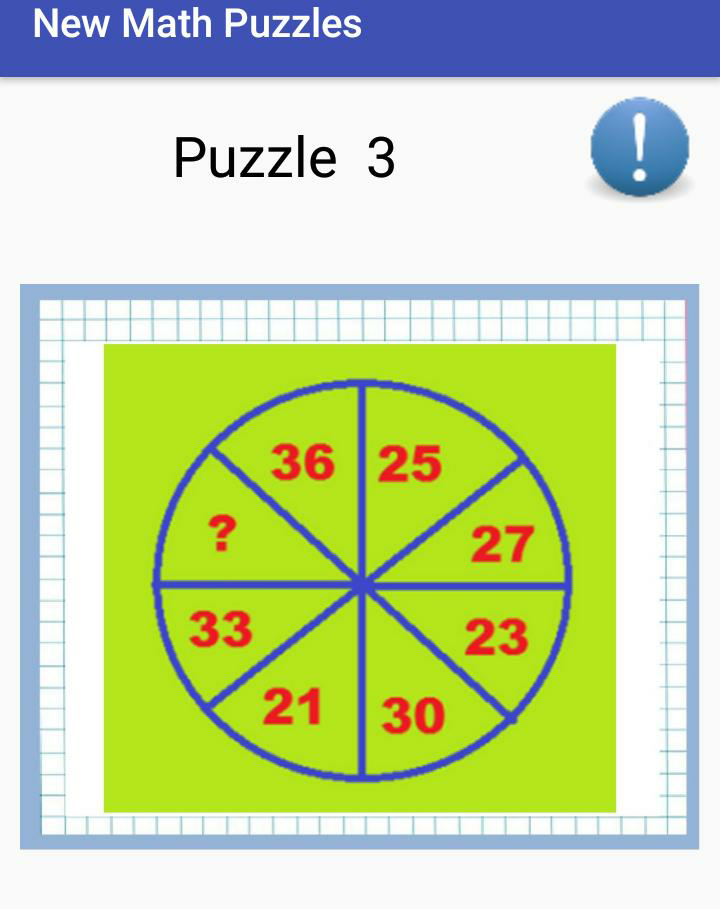
Question Number 40732 Answers: 1 Comments: 2

Question Number 40717 Answers: 1 Comments: 1
Question Number 40716 Answers: 2 Comments: 0
$$\int\left({cosx}−{cos}\mathrm{2}{x}/\mathrm{1}−{cosx}\right){dx} \\ $$
Question Number 40715 Answers: 1 Comments: 1
$$\mathrm{for}\:\mathrm{x}\geqslant\mathrm{2}\:\mid\mathrm{x}−\mathrm{2}\mid= \\ $$
Question Number 40711 Answers: 1 Comments: 0
Question Number 40709 Answers: 1 Comments: 1
Pg 1674 Pg 1675 Pg 1676 Pg 1677 Pg 1678 Pg 1679 Pg 1680 Pg 1681 Pg 1682 Pg 1683
