Question and Answers Forum

AllQuestion and Answers: Page 1678

Question Number 40889 Answers: 1 Comments: 0

prove?that ∫_0 ^1 ((1−(1−t)^n )/t)dt =Σ_(k=1) ^n (1/k)

$${prove}?{that} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\mathrm{1}−\left(\mathrm{1}−{t}\right)^{{n}} }{{t}}{dt}\:=\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{{k}} \\ $$

Question Number 40888 Answers: 0 Comments: 0

prove that ∀ξ ∈]0,π[ ∣∫_ξ ^π (((sint)/t))^n dt∣≤π(((sinξ)/ξ))^n n integr natural

$$\left.{prove}\:{that}\:\forall\xi\:\in\right]\mathrm{0},\pi\left[\right. \\ $$$$\mid\int_{\xi} ^{\pi} \left(\frac{{sint}}{{t}}\right)^{{n}} {dt}\mid\leqslant\pi\left(\frac{{sin}\xi}{\xi}\right)^{{n}} \:\:{n}\:{integr}\:{natural} \\ $$

Question Number 40887 Answers: 0 Comments: 1

calculate ∫_0 ^1 ((tln(t))/(t^2 −1))dt

$${calculate}\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{tln}\left({t}\right)}{{t}^{\mathrm{2}} −\mathrm{1}}{dt} \\ $$

Question Number 40886 Answers: 0 Comments: 0

prove that ∫_0 ^1 ((t^(2p+1) ln(t))/(t^2 −1))dt =(π^2 /(24)) −(1/4)Σ_(k=1) ^p (1/k^2 )

$${prove}\:{that}\: \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{t}^{\mathrm{2}{p}+\mathrm{1}} {ln}\left({t}\right)}{{t}^{\mathrm{2}} −\mathrm{1}}{dt}\:=\frac{\pi^{\mathrm{2}} }{\mathrm{24}}\:−\frac{\mathrm{1}}{\mathrm{4}}\sum_{{k}=\mathrm{1}} ^{{p}} \:\frac{\mathrm{1}}{{k}^{\mathrm{2}} } \\ $$

Question Number 40885 Answers: 0 Comments: 1

prove that 1) ∫_0 ^1 ((t^p ln(t))/(t−1))dt =(π^2 /6) −Σ_(k=1) ^p (1/k^2 ) 2) ∫_0 ^1 ((t^(2p) ln(t))/(t^2 −1))dt =(π^2 /8) −Σ_(k=0) ^(p−1) (1/((2k+1)^2 ))

$${prove}\:{that} \\ $$$$\left.\mathrm{1}\right)\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{t}^{{p}} {ln}\left({t}\right)}{{t}−\mathrm{1}}{dt}\:=\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\:−\sum_{{k}=\mathrm{1}} ^{{p}} \:\frac{\mathrm{1}}{{k}^{\mathrm{2}} } \\ $$$$\left.\mathrm{2}\right)\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{t}^{\mathrm{2}{p}} {ln}\left({t}\right)}{{t}^{\mathrm{2}} −\mathrm{1}}{dt}\:=\frac{\pi^{\mathrm{2}} }{\mathrm{8}}\:−\sum_{{k}=\mathrm{0}} ^{{p}−\mathrm{1}} \:\:\frac{\mathrm{1}}{\left(\mathrm{2}{k}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$

Question Number 40884 Answers: 2 Comments: 0

1) fond ∫_0 ^1 ((ln(t))/(t^2 −1))dt 2) find ∫_0 ^1 ((ln(t))/(t^4 −1))dt

$$\left.\mathrm{1}\right)\:{fond}\:\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left({t}\right)}{{t}^{\mathrm{2}} −\mathrm{1}}{dt} \\ $$$$\left.\mathrm{2}\right)\:{find}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{ln}\left({t}\right)}{{t}^{\mathrm{4}} −\mathrm{1}}{dt} \\ $$

Question Number 40883 Answers: 1 Comments: 0

find ∫_0 ^∞ (t^p /(e^t −1))dt with p∈N^★

$${find}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{t}^{{p}} }{{e}^{{t}} −\mathrm{1}}{dt}\:{with}\:{p}\in{N}^{\bigstar} \\ $$

Question Number 40882 Answers: 0 Comments: 0

1)prove that ∀n≥2(n inyegr) x^(2n) −1=(x−1)(x+1)Π_(k=1) ^(n−1) (x^2 −2cos(((kπ)/n))x+1) 2)find the value of ∫_0 ^π ln(x^2 −2xcost +1)dt

$$\left.\mathrm{1}\right){prove}\:{that}\:\forall{n}\geqslant\mathrm{2}\left({n}\:{inyegr}\right) \\ $$$${x}^{\mathrm{2}{n}} −\mathrm{1}=\left({x}−\mathrm{1}\right)\left({x}+\mathrm{1}\right)\prod_{{k}=\mathrm{1}} ^{{n}−\mathrm{1}} \left({x}^{\mathrm{2}} \:−\mathrm{2}{cos}\left(\frac{{k}\pi}{{n}}\right){x}+\mathrm{1}\right) \\ $$$$\left.\mathrm{2}\right){find}\:{the}\:{value}\:{of}\:\:\int_{\mathrm{0}} ^{\pi} {ln}\left({x}^{\mathrm{2}} −\mathrm{2}{xcost}\:+\mathrm{1}\right){dt} \\ $$

Question Number 40880 Answers: 0 Comments: 0

prove that Σ_(k=n) ^∞ (1/k^α ) ∼ (1/((α−1)n^(α−1) ))with α>1

$${prove}\:{that}\:\sum_{{k}={n}} ^{\infty} \:\frac{\mathrm{1}}{{k}^{\alpha} }\:\sim\:\:\frac{\mathrm{1}}{\left(\alpha−\mathrm{1}\right){n}^{\alpha−\mathrm{1}} }{with}\:\alpha>\mathrm{1} \\ $$

Question Number 40878 Answers: 0 Comments: 0

let u_0 >0 and ∀n∈N u_(n+1) =u_n +(1/u_n ) 1) prove that (u_n )is increasing and lim u_n =+∞ 2)by consideringthe functionϕ(t)=(1/(2t+x)) prove that ∀n∈N Σ_(k=1) ^n (1/(2k+x)) ≤(1/2)ln(1+((2n)/x)) 3)find a equivalent of u_n (n→+∞)

$${let}\:{u}_{\mathrm{0}} >\mathrm{0}\:{and}\:\forall{n}\in{N} \\ $$$${u}_{{n}+\mathrm{1}} ={u}_{{n}} \:+\frac{\mathrm{1}}{{u}_{{n}} } \\ $$$$\left.\mathrm{1}\right)\:{prove}\:{that}\:\left({u}_{{n}} \right){is}\:{increasing}\:{and}\:{lim}\:{u}_{{n}} \:=+\infty \\ $$$$\left.\mathrm{2}\right){by}\:{consideringthe}\:{function}\varphi\left({t}\right)=\frac{\mathrm{1}}{\mathrm{2}{t}+{x}} \\ $$$${prove}\:{that}\:\forall{n}\in{N}\:\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{\mathrm{2}{k}+{x}}\:\leqslant\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{1}+\frac{\mathrm{2}{n}}{{x}}\right) \\ $$$$\left.\mathrm{3}\right){find}\:{a}\:{equivalent}\:{of}\:{u}_{{n}} \left({n}\rightarrow+\infty\right) \\ $$

Question Number 40876 Answers: 0 Comments: 0

prove by recurrence that Σ_(k=1) ^n k^4 =((n(n+1)(2n+1)(3n^2 +3n−1))/(30))

$${prove}\:{by}\:{recurrence}\:{that}\: \\ $$$$\sum_{{k}=\mathrm{1}} ^{{n}} \:{k}^{\mathrm{4}} =\frac{{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)\left(\mathrm{3}{n}^{\mathrm{2}} \:+\mathrm{3}{n}−\mathrm{1}\right)}{\mathrm{30}} \\ $$

Question Number 40875 Answers: 1 Comments: 0

2a sin(((25)/a)) − 51 = 0, find a

$$\mathrm{2a}\:\mathrm{sin}\left(\frac{\mathrm{25}}{\mathrm{a}}\right)\:−\:\mathrm{51}\:=\:\mathrm{0},\:\:\mathrm{find}\:\mathrm{a} \\ $$

Question Number 40874 Answers: 0 Comments: 0

Question Number 40873 Answers: 1 Comments: 0

If a^3 +b^3 =0, prove that log (a+b)=(1/2)(log a +log b +log 3) [given a+b≠0]

$${If}\:{a}^{\mathrm{3}} +{b}^{\mathrm{3}} =\mathrm{0},\:\:{prove}\:{that}\:\mathrm{log}\:\left({a}+{b}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{log}\:{a}\:+\mathrm{log}\:{b}\:+\mathrm{log}\:\mathrm{3}\right) \\ $$$$\left[{given}\:{a}+{b}\neq\mathrm{0}\right] \\ $$

Question Number 40872 Answers: 1 Comments: 2

If a^3 +b^3 =0, prove that log (a+b)=(1/2)(log a +log b +log 3) [given a+b≠0]

Question Number 40870 Answers: 1 Comments: 1

fnd ∫ (1+(1/x^2 ))arctan(x−(1/x))dx .

$${fnd}\:\:\int\:\:\left(\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right){arctan}\left({x}−\frac{\mathrm{1}}{{x}}\right){dx}\:. \\ $$

Question Number 40868 Answers: 0 Comments: 4

calculate ∫_0 ^(π/2) (x/(sinx))dx .

$${calculate}\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{{x}}{{sinx}}{dx}\:\:. \\ $$

Question Number 40867 Answers: 0 Comments: 1

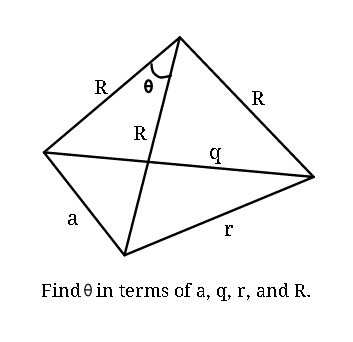
Question Number 40857 Answers: 1 Comments: 2

Question Number 40847 Answers: 1 Comments: 0

If the coordinate of the points A and B be (3,3) and (7,6) then the length of the portion of the line AB intercepted between the axes is (a) (5/4) (b) ((√(10))/4) (c) ((√(13))/3) (d) none

$${If}\:{the}\:{coordinate}\:{of}\:{the}\:{points}\:{A}\: \\ $$$${and}\:{B}\:{be}\:\left(\mathrm{3},\mathrm{3}\right)\:{and}\:\left(\mathrm{7},\mathrm{6}\right)\:{then}\:{the} \\ $$$${length}\:{of}\:{the}\:{portion}\:{of}\:{the}\:{line}\: \\ $$$${AB}\:{intercepted}\:{between}\:{the}\:{axes}\:{is} \\ $$$$\left({a}\right)\:\:\frac{\mathrm{5}}{\mathrm{4}}\:\:\:\left({b}\right)\:\:\:\frac{\sqrt{\mathrm{10}}}{\mathrm{4}}\:\:\:\:\left({c}\right)\:\:\frac{\sqrt{\mathrm{13}}}{\mathrm{3}}\:\:\:\:\left({d}\right)\:{none} \\ $$

Question Number 40830 Answers: 0 Comments: 1

find ∫ (√(2+tan^2 t))dt

$${find}\:\int\:\sqrt{\mathrm{2}+{tan}^{\mathrm{2}} {t}}{dt} \\ $$

Question Number 40829 Answers: 1 Comments: 0

let f(t) = ∫_0 ^∞ ((arctan(tx))/(x^3 +8))dx 1)find a simple form of f(t) 2)calculate ∫_0 ^∞ ((arctan(x))/(x^3 +8))dx .

$${let}\:{f}\left({t}\right)\:=\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{arctan}\left({tx}\right)}{{x}^{\mathrm{3}} +\mathrm{8}}{dx} \\ $$$$\left.\mathrm{1}\right){find}\:{a}\:{simple}\:{form}\:{of}\:{f}\left({t}\right) \\ $$$$\left.\mathrm{2}\right){calculate}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{arctan}\left({x}\right)}{{x}^{\mathrm{3}} \:+\mathrm{8}}{dx}\:. \\ $$

Question Number 40826 Answers: 1 Comments: 0

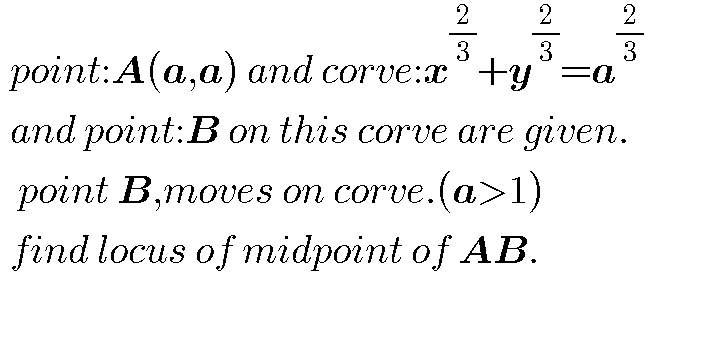
Question Number 40823 Answers: 0 Comments: 1

calculate ∫_0 ^(π/2) (√(cos^2 x +3sin^2 x))dx

$${calculate}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \sqrt{{cos}^{\mathrm{2}} {x}\:+\mathrm{3}{sin}^{\mathrm{2}} {x}}{dx} \\ $$

Question Number 40822 Answers: 2 Comments: 0

Question Number 40818 Answers: 1 Comments: 0

Two large parallel metal plates carrying opposite charges are seperated by a distance of 0.2m,and the potential difference between them is 0.5KV. (a)Calculate the magnitude of the uniform electric field between them. (b)Also calculate the workdone by this field on a charge of 4.0×10^(−9) C when it moves from the plate of higher potential to that of lower potential.

$${Two}\:{large}\:{parallel}\:{metal}\:{plates}\:{carrying} \\ $$$${opposite}\:{charges}\:{are}\:{seperated}\:{by}\:{a} \\ $$$${distance}\:{of}\:\mathrm{0}.\mathrm{2}{m},{and}\:{the}\:{potential} \\ $$$${difference}\:{between}\:{them}\:{is}\:\mathrm{0}.\mathrm{5}{KV}. \\ $$$$\left({a}\right){Calculate}\:{the}\:{magnitude}\:{of}\:{the} \\ $$$${uniform}\:{electric}\:{field}\:{between}\:{them}. \\ $$$$\left({b}\right){Also}\:{calculate}\:{the}\:{workdone}\:{by} \\ $$$${this}\:{field}\:{on}\:{a}\:{charge}\:{of}\:\mathrm{4}.\mathrm{0}×\mathrm{10}^{−\mathrm{9}} {C} \\ $$$${when}\:{it}\:{moves}\:{from}\:{the}\:{plate}\:{of} \\ $$$${higher}\:{potential}\:{to}\:{that}\:{of}\:{lower} \\ $$$${potential}. \\ $$

Pg 1673 Pg 1674 Pg 1675 Pg 1676 Pg 1677 Pg 1678 Pg 1679 Pg 1680 Pg 1681 Pg 1682

Contact: info@tinkutara.com