
AllQuestion and Answers: Page 1677
Question Number 41236 Answers: 2 Comments: 0
Question Number 41233 Answers: 2 Comments: 1
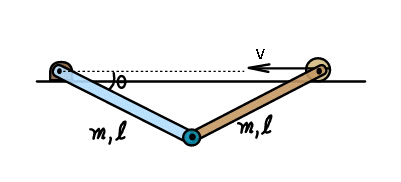
Question Number 41231 Answers: 1 Comments: 1
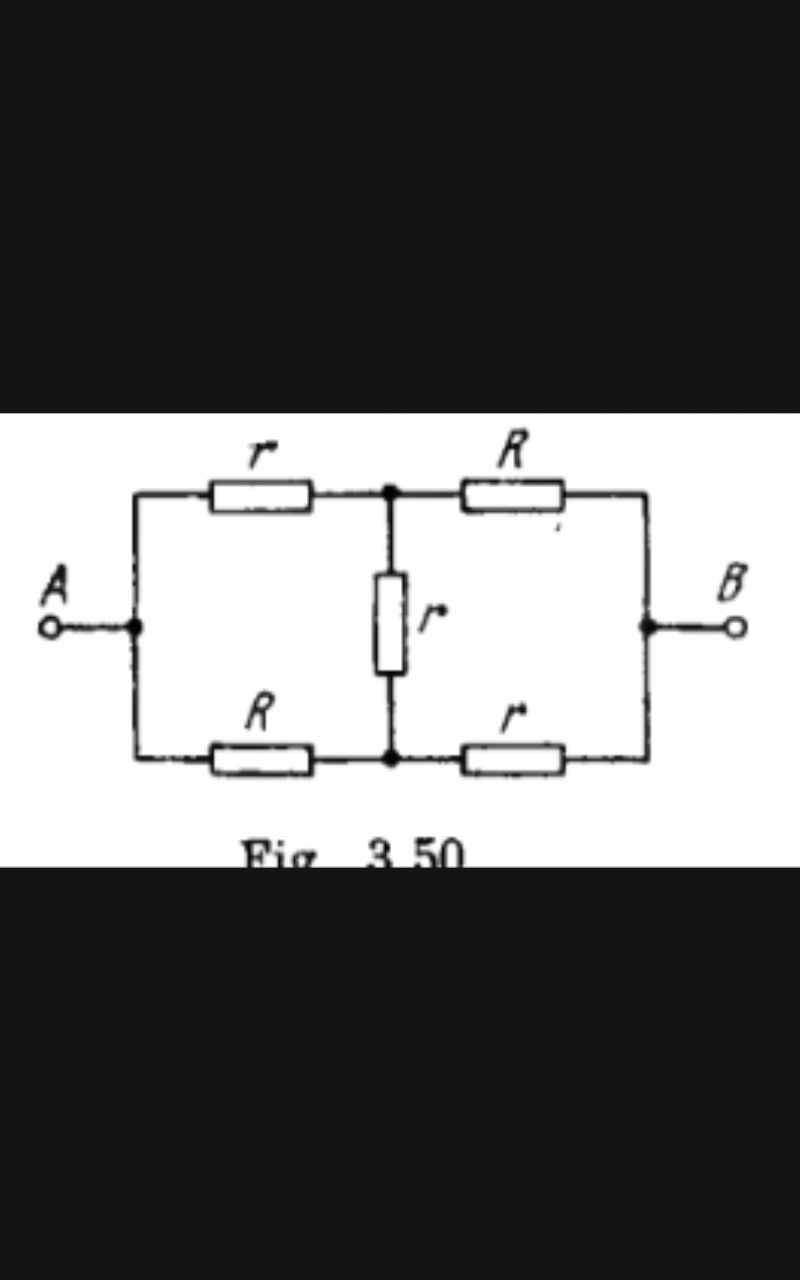
Question Number 41214 Answers: 3 Comments: 1
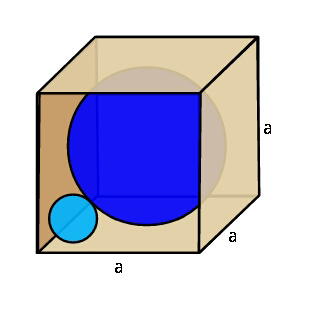
Question Number 41203 Answers: 1 Comments: 5
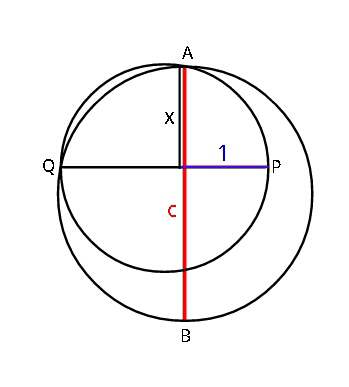
Question Number 41174 Answers: 1 Comments: 0

Question Number 41167 Answers: 1 Comments: 0
Question Number 41160 Answers: 3 Comments: 3

Question Number 41157 Answers: 2 Comments: 3
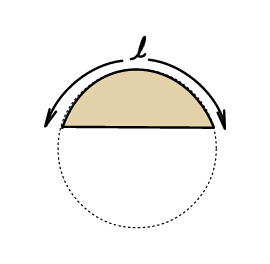
Question Number 41198 Answers: 2 Comments: 3
$$\mathrm{evaluate}\:\boldsymbol{\mathrm{ln}}\left(−\mathrm{1}\right) \\ $$
Question Number 41151 Answers: 1 Comments: 2
Question Number 41148 Answers: 1 Comments: 0
Question Number 41146 Answers: 1 Comments: 1

Question Number 41141 Answers: 0 Comments: 1
Question Number 41139 Answers: 1 Comments: 1

Question Number 41138 Answers: 0 Comments: 3
Question Number 41137 Answers: 0 Comments: 0

Question Number 41136 Answers: 1 Comments: 0
Question Number 41135 Answers: 1 Comments: 0
Question Number 41117 Answers: 2 Comments: 0

Question Number 41121 Answers: 0 Comments: 0
Question Number 41122 Answers: 0 Comments: 0
Question Number 41108 Answers: 1 Comments: 0
Question Number 41103 Answers: 1 Comments: 6

Question Number 41101 Answers: 1 Comments: 2
Question Number 41096 Answers: 0 Comments: 1

Pg 1672 Pg 1673 Pg 1674 Pg 1675 Pg 1676 Pg 1677 Pg 1678 Pg 1679 Pg 1680 Pg 1681
