
AllQuestion and Answers: Page 1674
Question Number 41858 Answers: 0 Comments: 3
$${i}\:{have}\:{fever}...{so}\:{brain}\:{activity}\:{got}\:{reduced}... \\ $$
Question Number 41856 Answers: 1 Comments: 0

Question Number 41855 Answers: 0 Comments: 1
Question Number 41854 Answers: 0 Comments: 0
Question Number 41851 Answers: 0 Comments: 2

Question Number 41847 Answers: 1 Comments: 0
Question Number 41846 Answers: 1 Comments: 0
Question Number 41845 Answers: 1 Comments: 0
Question Number 41848 Answers: 0 Comments: 3
Question Number 42310 Answers: 1 Comments: 1

Question Number 41828 Answers: 1 Comments: 0
Question Number 41824 Answers: 3 Comments: 0
Question Number 41820 Answers: 1 Comments: 0
Question Number 41813 Answers: 1 Comments: 0
Question Number 41806 Answers: 1 Comments: 1
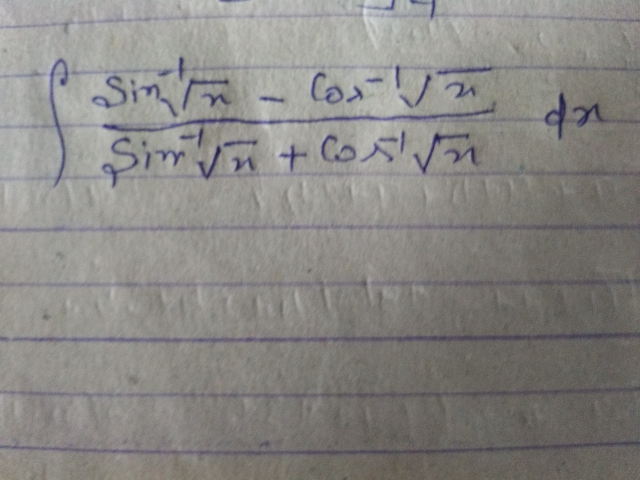
Question Number 41798 Answers: 0 Comments: 5
Question Number 41797 Answers: 1 Comments: 0
Question Number 41796 Answers: 2 Comments: 0
Question Number 41780 Answers: 2 Comments: 0

Question Number 41766 Answers: 2 Comments: 0

Question Number 41765 Answers: 2 Comments: 0
Question Number 41762 Answers: 0 Comments: 3
Question Number 41761 Answers: 1 Comments: 0
Question Number 41757 Answers: 0 Comments: 0
Question Number 41744 Answers: 1 Comments: 0

Question Number 41754 Answers: 3 Comments: 0

Pg 1669 Pg 1670 Pg 1671 Pg 1672 Pg 1673 Pg 1674 Pg 1675 Pg 1676 Pg 1677 Pg 1678
