
AllQuestion and Answers: Page 1673
Question Number 41517 Answers: 1 Comments: 1
Question Number 41516 Answers: 1 Comments: 1
Question Number 41515 Answers: 1 Comments: 3
Question Number 41514 Answers: 1 Comments: 0
Question Number 41513 Answers: 2 Comments: 0
Question Number 41512 Answers: 0 Comments: 0
Question Number 41508 Answers: 0 Comments: 0
Question Number 41495 Answers: 2 Comments: 3
Question Number 41488 Answers: 2 Comments: 0

Question Number 41487 Answers: 3 Comments: 4

Question Number 41461 Answers: 1 Comments: 3
Question Number 41459 Answers: 0 Comments: 1

Question Number 41454 Answers: 1 Comments: 1
Question Number 41447 Answers: 1 Comments: 0

Question Number 41444 Answers: 0 Comments: 1
Question Number 41443 Answers: 1 Comments: 0
Question Number 41479 Answers: 1 Comments: 0

Question Number 41436 Answers: 4 Comments: 0

Question Number 41434 Answers: 1 Comments: 1
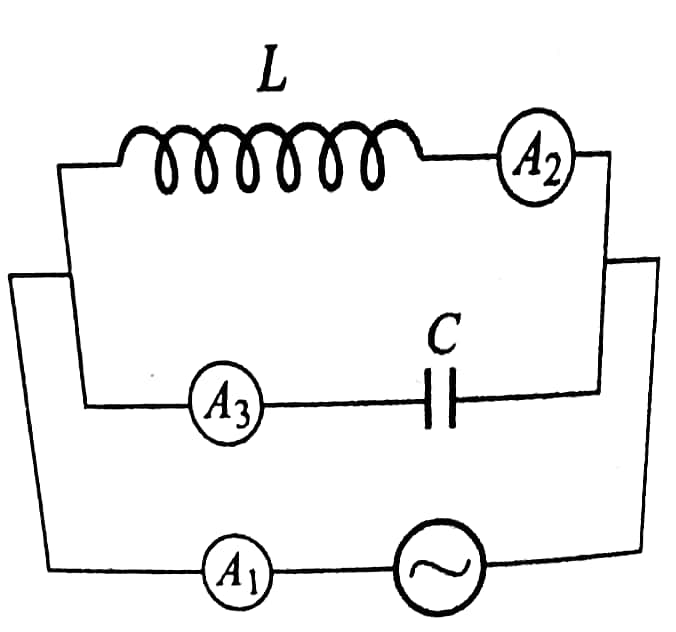
Question Number 41431 Answers: 0 Comments: 3

Question Number 41410 Answers: 0 Comments: 2
Question Number 41409 Answers: 1 Comments: 0
Question Number 41408 Answers: 0 Comments: 1
Question Number 41407 Answers: 0 Comments: 1
Question Number 41394 Answers: 1 Comments: 1
Question Number 41392 Answers: 0 Comments: 1
Pg 1668 Pg 1669 Pg 1670 Pg 1671 Pg 1672 Pg 1673 Pg 1674 Pg 1675 Pg 1676 Pg 1677
