
AllQuestion and Answers: Page 1670
Question Number 42207 Answers: 1 Comments: 0
Question Number 42200 Answers: 1 Comments: 0
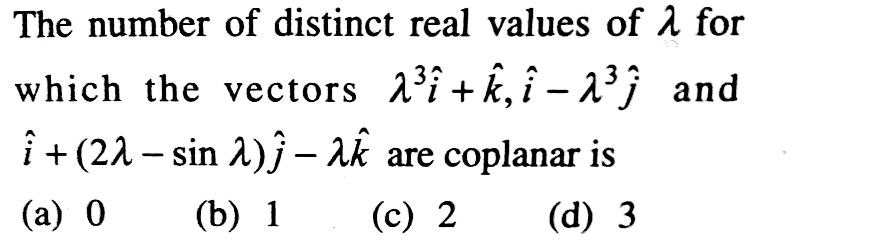
Question Number 42199 Answers: 1 Comments: 0

Question Number 42196 Answers: 0 Comments: 4
Question Number 42195 Answers: 1 Comments: 0
Question Number 42410 Answers: 1 Comments: 1
Question Number 42191 Answers: 0 Comments: 1
Question Number 42190 Answers: 0 Comments: 1
Question Number 42189 Answers: 0 Comments: 0
Question Number 42188 Answers: 0 Comments: 1
Question Number 42187 Answers: 0 Comments: 1
Question Number 42182 Answers: 0 Comments: 3
Question Number 42232 Answers: 1 Comments: 0
Question Number 42180 Answers: 1 Comments: 0
Question Number 42176 Answers: 0 Comments: 1
Question Number 42175 Answers: 0 Comments: 0
Question Number 42174 Answers: 1 Comments: 0
$${cos}^{\mathrm{2}} \mathrm{3}{xcos}\mathrm{2}{x}−{cos}^{\mathrm{2}} {x}=\mathrm{0} \\ $$
Question Number 42170 Answers: 1 Comments: 0
Question Number 42169 Answers: 0 Comments: 0
Question Number 42157 Answers: 0 Comments: 3
Question Number 42154 Answers: 0 Comments: 5

Question Number 42150 Answers: 0 Comments: 0
Question Number 42145 Answers: 1 Comments: 2

Question Number 42133 Answers: 1 Comments: 0
Question Number 42131 Answers: 1 Comments: 1
Question Number 42128 Answers: 0 Comments: 2
Pg 1665 Pg 1666 Pg 1667 Pg 1668 Pg 1669 Pg 1670 Pg 1671 Pg 1672 Pg 1673 Pg 1674
