
AllQuestion and Answers: Page 1669
Question Number 42408 Answers: 0 Comments: 2
Question Number 42407 Answers: 1 Comments: 1
$$\int\:\frac{\mathrm{1}}{\mathrm{1}\:+\:\mathrm{tanx}}\:\mathrm{dx} \\ $$
Question Number 42402 Answers: 0 Comments: 0
Question Number 42395 Answers: 0 Comments: 1
Question Number 42394 Answers: 1 Comments: 1
Question Number 42392 Answers: 1 Comments: 1
$${calculate}\:\int\:\:\:\frac{{lnx}}{{x}\:+{x}\left({lnx}\right)^{\mathrm{2}} }{dx} \\ $$
Question Number 42391 Answers: 1 Comments: 1
Question Number 42375 Answers: 1 Comments: 5
Question Number 42374 Answers: 0 Comments: 1
Question Number 42370 Answers: 1 Comments: 1

Question Number 42367 Answers: 1 Comments: 0
Question Number 42366 Answers: 1 Comments: 0
Question Number 42364 Answers: 0 Comments: 3
Question Number 42401 Answers: 0 Comments: 1
Question Number 42400 Answers: 0 Comments: 0
Question Number 42358 Answers: 1 Comments: 0
Question Number 42357 Answers: 1 Comments: 0

Question Number 42352 Answers: 1 Comments: 0

Question Number 42345 Answers: 1 Comments: 2
Question Number 42336 Answers: 0 Comments: 0
Question Number 42332 Answers: 0 Comments: 0

Question Number 42331 Answers: 1 Comments: 0

Question Number 42330 Answers: 0 Comments: 0
Question Number 42340 Answers: 2 Comments: 3
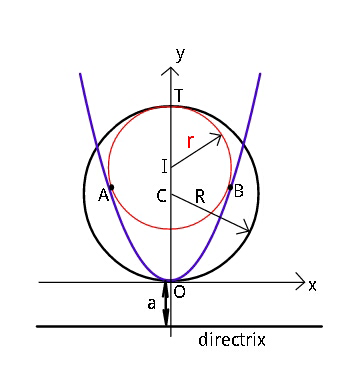
Question Number 42320 Answers: 1 Comments: 3

Question Number 42316 Answers: 1 Comments: 2

Pg 1664 Pg 1665 Pg 1666 Pg 1667 Pg 1668 Pg 1669 Pg 1670 Pg 1671 Pg 1672 Pg 1673
