
AllQuestion and Answers: Page 1668
Question Number 42494 Answers: 1 Comments: 1
Question Number 42493 Answers: 0 Comments: 1
Question Number 42492 Answers: 2 Comments: 0
Question Number 42490 Answers: 0 Comments: 0
$${find}\:{L}\left({arctanx}\right)\:\:.{L}\:{means}\:{laplace}\:{transform}\:. \\ $$
Question Number 42489 Answers: 0 Comments: 1
Question Number 42488 Answers: 1 Comments: 1
Question Number 42487 Answers: 0 Comments: 3
Question Number 42479 Answers: 1 Comments: 0
Question Number 42481 Answers: 0 Comments: 0
Question Number 42482 Answers: 0 Comments: 3
Question Number 42475 Answers: 0 Comments: 1
Question Number 42474 Answers: 0 Comments: 0

Question Number 42473 Answers: 0 Comments: 0

Question Number 42472 Answers: 0 Comments: 0

Question Number 42471 Answers: 0 Comments: 0
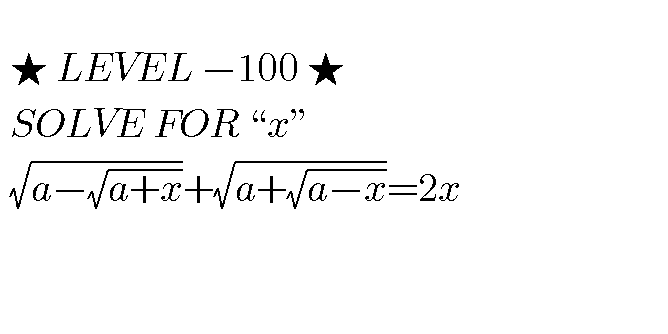
Question Number 42470 Answers: 0 Comments: 0

Question Number 42469 Answers: 0 Comments: 0
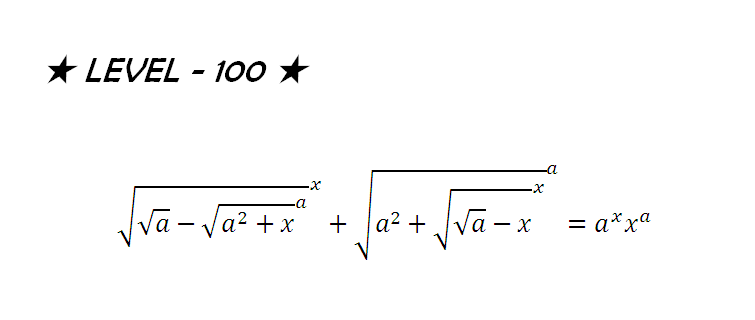
Question Number 42468 Answers: 0 Comments: 0

Question Number 42463 Answers: 1 Comments: 1
Question Number 42458 Answers: 0 Comments: 0
Question Number 42448 Answers: 3 Comments: 0

Question Number 42446 Answers: 2 Comments: 1
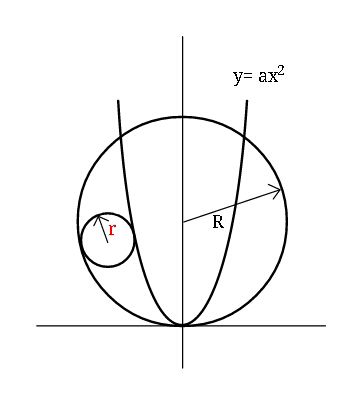
Question Number 42445 Answers: 0 Comments: 0
Question Number 42435 Answers: 1 Comments: 1
Question Number 42430 Answers: 1 Comments: 2
$${find}\:\int\:\:\:\:\:\:\:\frac{{dx}}{\mathrm{3}+{tan}^{\mathrm{2}} {x}} \\ $$
Question Number 42422 Answers: 1 Comments: 2

Pg 1663 Pg 1664 Pg 1665 Pg 1666 Pg 1667 Pg 1668 Pg 1669 Pg 1670 Pg 1671 Pg 1672
