
AllQuestion and Answers: Page 1667
Question Number 42583 Answers: 0 Comments: 6
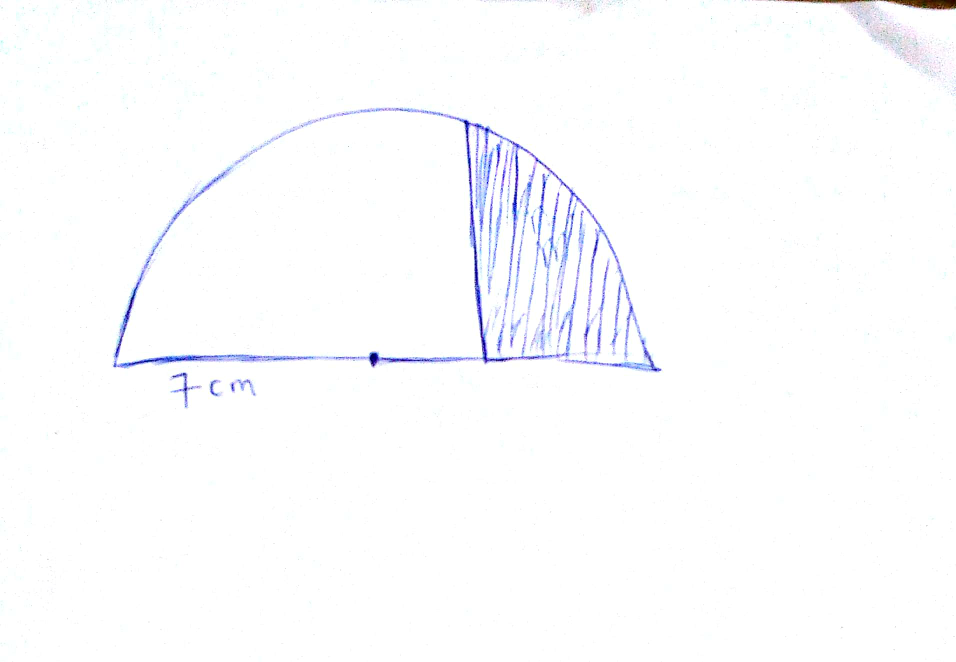
Question Number 42580 Answers: 1 Comments: 1
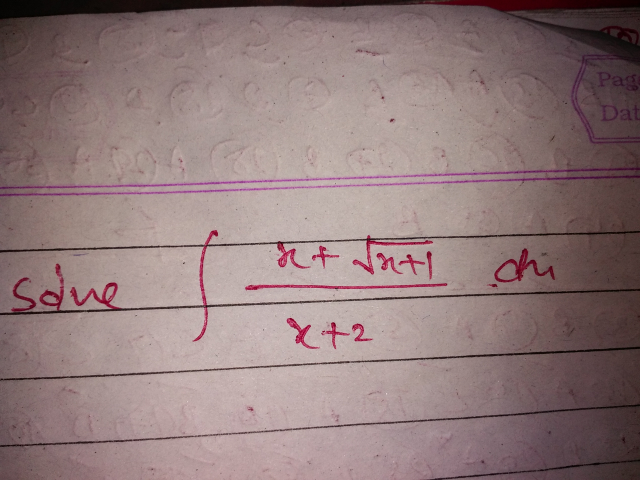
Question Number 42579 Answers: 1 Comments: 1
Question Number 42559 Answers: 5 Comments: 0

Question Number 42553 Answers: 0 Comments: 1
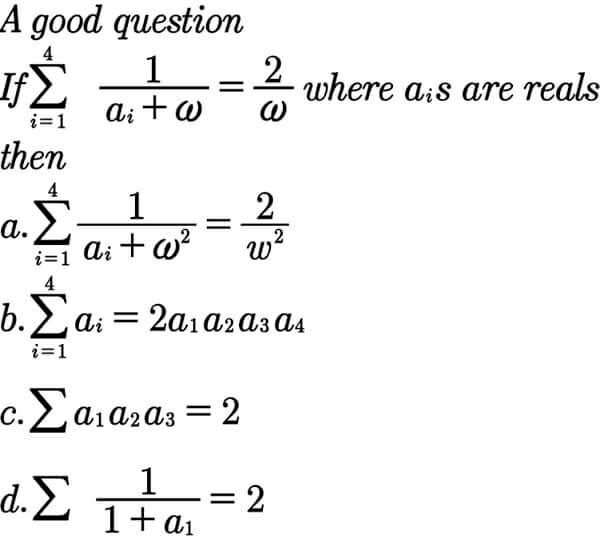
Question Number 42550 Answers: 1 Comments: 3
$$\mathrm{2}^{\frac{\mathrm{1}}{{x}}} =\sqrt{{x}} \\ $$$${Find}\:{x} \\ $$
Question Number 43535 Answers: 2 Comments: 2
Question Number 42549 Answers: 1 Comments: 0
Question Number 42543 Answers: 0 Comments: 3

Question Number 42538 Answers: 1 Comments: 1
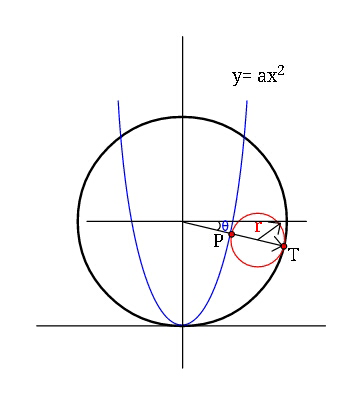
Question Number 43537 Answers: 0 Comments: 1
Question Number 42521 Answers: 1 Comments: 0
Question Number 42520 Answers: 1 Comments: 0
Question Number 42519 Answers: 1 Comments: 0
Question Number 42516 Answers: 1 Comments: 1
Question Number 42514 Answers: 1 Comments: 0
Question Number 42508 Answers: 2 Comments: 0
Question Number 42507 Answers: 0 Comments: 2
Question Number 42506 Answers: 0 Comments: 1
Question Number 42505 Answers: 0 Comments: 2
Question Number 42504 Answers: 0 Comments: 1
Question Number 42503 Answers: 1 Comments: 1
Question Number 42502 Answers: 0 Comments: 0
Question Number 42501 Answers: 0 Comments: 1
Question Number 42500 Answers: 0 Comments: 2
Question Number 42497 Answers: 0 Comments: 1
Pg 1662 Pg 1663 Pg 1664 Pg 1665 Pg 1666 Pg 1667 Pg 1668 Pg 1669 Pg 1670 Pg 1671
