
AllQuestion and Answers: Page 1666
Question Number 42671 Answers: 0 Comments: 0
Question Number 42670 Answers: 1 Comments: 3
Question Number 42698 Answers: 1 Comments: 0
Question Number 42668 Answers: 0 Comments: 0
Question Number 42708 Answers: 0 Comments: 1
Question Number 42663 Answers: 0 Comments: 0
Question Number 42657 Answers: 0 Comments: 0
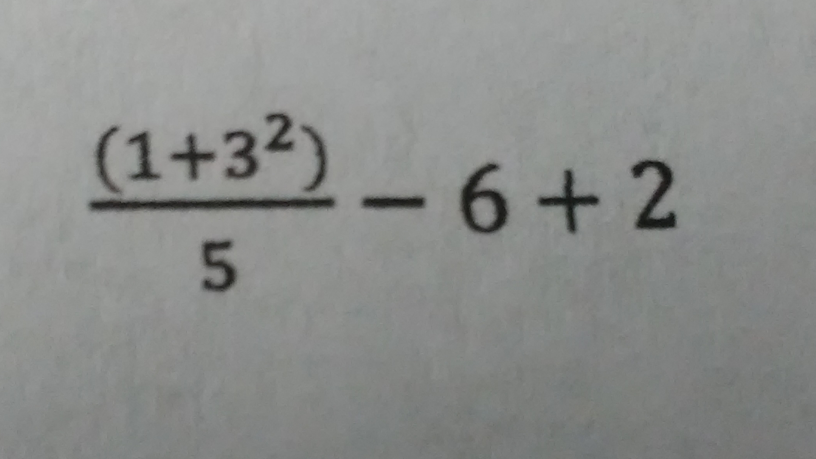
Question Number 42656 Answers: 1 Comments: 0

Question Number 42654 Answers: 2 Comments: 2
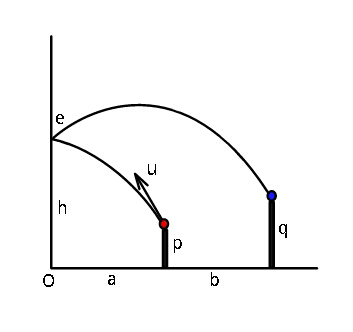
Question Number 42650 Answers: 0 Comments: 0
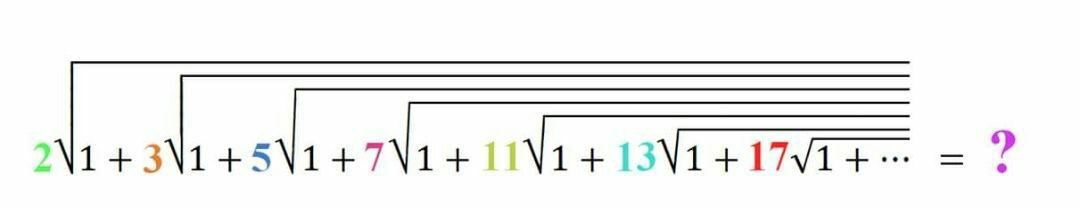
Question Number 42649 Answers: 0 Comments: 0

Question Number 42648 Answers: 0 Comments: 0

Question Number 42639 Answers: 0 Comments: 0
Question Number 42636 Answers: 0 Comments: 1
Question Number 42631 Answers: 1 Comments: 7
Question Number 42630 Answers: 0 Comments: 0
Question Number 42629 Answers: 0 Comments: 0
Question Number 42628 Answers: 0 Comments: 2
Question Number 42627 Answers: 2 Comments: 0
Question Number 42624 Answers: 1 Comments: 2

Question Number 42622 Answers: 0 Comments: 1
$${find}\:\int\:\:{th}\left(\mathrm{2}{x}+\mathrm{1}\right){dx}\: \\ $$
Question Number 42621 Answers: 0 Comments: 1
Question Number 42605 Answers: 0 Comments: 3
Question Number 42603 Answers: 0 Comments: 2
Question Number 42593 Answers: 1 Comments: 1
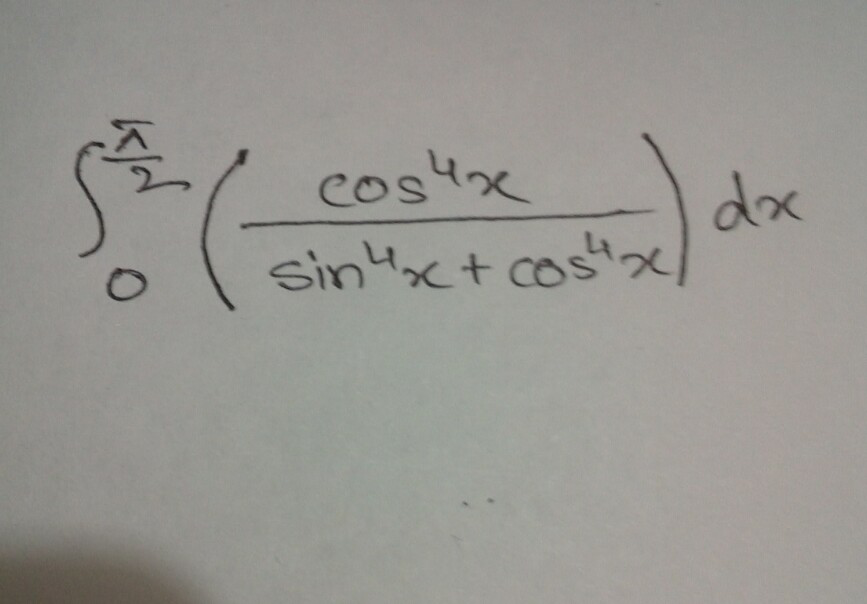
Question Number 42592 Answers: 1 Comments: 0
Pg 1661 Pg 1662 Pg 1663 Pg 1664 Pg 1665 Pg 1666 Pg 1667 Pg 1668 Pg 1669 Pg 1670
