
AllQuestion and Answers: Page 1665
Question Number 42768 Answers: 0 Comments: 0

Question Number 42766 Answers: 0 Comments: 0
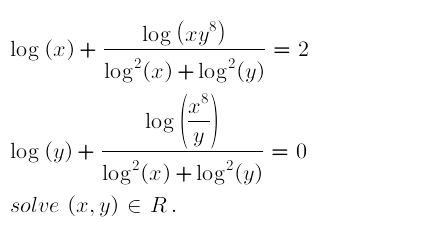
Question Number 42765 Answers: 0 Comments: 1

Question Number 42763 Answers: 0 Comments: 1
Question Number 42761 Answers: 0 Comments: 0
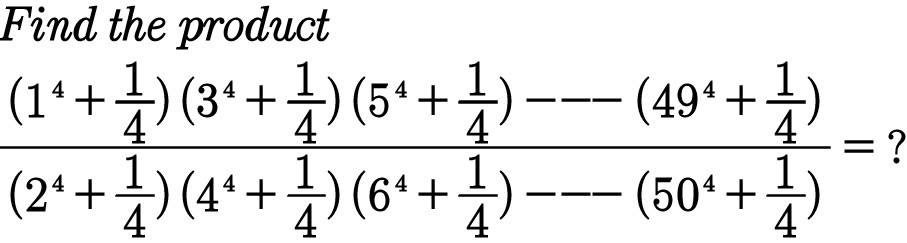
Question Number 42758 Answers: 0 Comments: 0

Question Number 42756 Answers: 0 Comments: 1
Question Number 42730 Answers: 1 Comments: 1
Question Number 42728 Answers: 2 Comments: 0
Question Number 42725 Answers: 1 Comments: 0
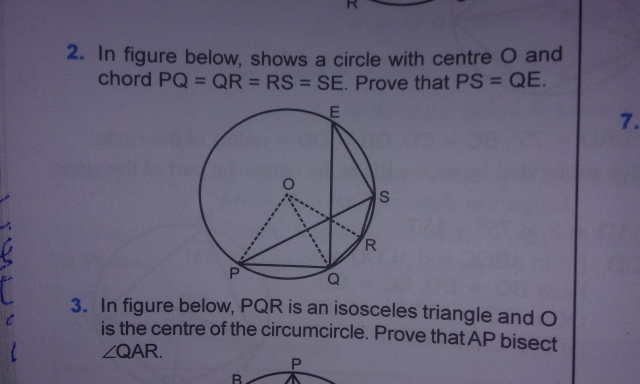
Question Number 42719 Answers: 0 Comments: 1

Question Number 42718 Answers: 0 Comments: 0
Question Number 42713 Answers: 1 Comments: 1

Question Number 42711 Answers: 1 Comments: 0
Question Number 42709 Answers: 1 Comments: 3
Question Number 42704 Answers: 0 Comments: 4
Question Number 42695 Answers: 0 Comments: 1
Question Number 42689 Answers: 0 Comments: 3
Question Number 42688 Answers: 0 Comments: 3
Question Number 42684 Answers: 0 Comments: 2
Question Number 42681 Answers: 0 Comments: 0

Question Number 42680 Answers: 0 Comments: 2
Question Number 42679 Answers: 0 Comments: 2
Question Number 42673 Answers: 1 Comments: 0
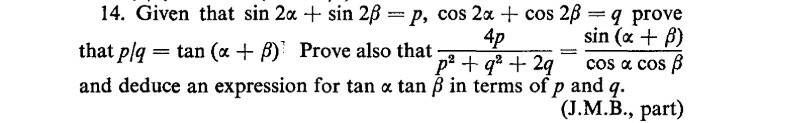
Question Number 42672 Answers: 0 Comments: 0
Question Number 42671 Answers: 0 Comments: 0
Pg 1660 Pg 1661 Pg 1662 Pg 1663 Pg 1664 Pg 1665 Pg 1666 Pg 1667 Pg 1668 Pg 1669
