Question and Answers Forum

AllQuestion and Answers: Page 1664

Question Number 42391 Answers: 1 Comments: 1

find the value of ∫_0 ^(π/4) ln(1+tanx)dx

$${find}\:{the}\:{value}\:{of}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left(\mathrm{1}+{tanx}\right){dx} \\ $$

Question Number 42375 Answers: 1 Comments: 5

Find value of α such that the following system has infinite many solutions x − 3z = −3 −2x − αy + z = 2 x + 2y + αz = 1

$$\mathrm{Find}\:\mathrm{value}\:\mathrm{of}\:\:\alpha\:\mathrm{such}\:\mathrm{that}\:\mathrm{the}\:\mathrm{following}\:\mathrm{system} \\ $$$$\mathrm{has}\:\mathrm{infinite}\:\mathrm{many}\:\mathrm{solutions} \\ $$$$ \\ $$$${x}\:−\:\mathrm{3}{z}\:=\:−\mathrm{3} \\ $$$$−\mathrm{2}{x}\:−\:\alpha{y}\:+\:{z}\:=\:\mathrm{2} \\ $$$${x}\:+\:\mathrm{2}{y}\:+\:\alpha{z}\:=\:\mathrm{1} \\ $$

Question Number 42374 Answers: 0 Comments: 1

let f(x) = ∫_0 ^∞ arctan(xt^2 )cos(t^2 ) dt 1) find a explicite form of f^′ (x) 2) find a explicite form of f(x) 3) find the value of ∫_0 ^∞ cos(t^2 ) arctan(t^2 )dt and ∫_0 ^∞ cos(t^2 )arctan(2t^2 )dt

$${let}\:{f}\left({x}\right)\:=\:\int_{\mathrm{0}} ^{\infty} \:\:\:{arctan}\left({xt}^{\mathrm{2}} \right){cos}\left({t}^{\mathrm{2}} \right)\:{dt} \\ $$$$\left.\mathrm{1}\right)\:{find}\:{a}\:{explicite}\:{form}\:{of}\:{f}^{'} \left({x}\right) \\ $$$$\left.\mathrm{2}\right)\:{find}\:{a}\:{explicite}\:{form}\:{of}\:{f}\left({x}\right) \\ $$$$\left.\mathrm{3}\right)\:{find}\:{the}\:{value}\:{of}\:\:\:\int_{\mathrm{0}} ^{\infty} \:\:{cos}\left({t}^{\mathrm{2}} \right)\:{arctan}\left({t}^{\mathrm{2}} \right){dt}\:\:\:{and}\:\:\int_{\mathrm{0}} ^{\infty} \:{cos}\left({t}^{\mathrm{2}} \right){arctan}\left(\mathrm{2}{t}^{\mathrm{2}} \right){dt} \\ $$

Question Number 42370 Answers: 1 Comments: 1

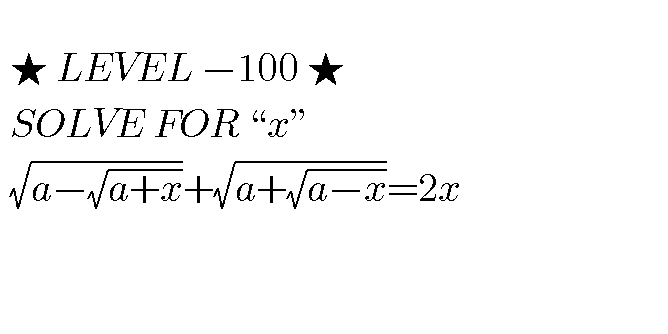
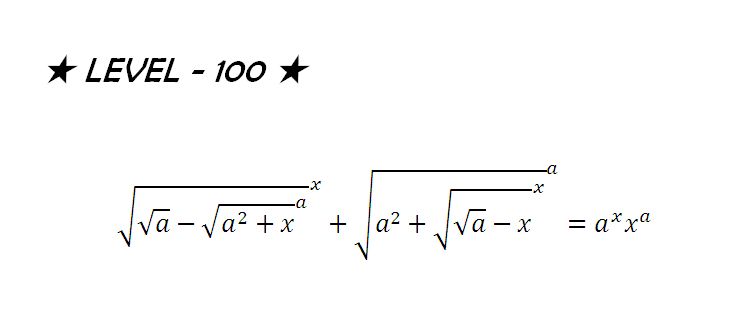
Question Number 42367 Answers: 1 Comments: 0

lim_(n→∞) ((( ((n),(0) ) ((n),(1) ) ((n),(2) )... ((n),(n) )))^(1/(n^2 +n)) )

$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\left(\sqrt[{{n}^{\mathrm{2}} +{n}}]{\:\begin{pmatrix}{{n}}\\{\mathrm{0}}\end{pmatrix}\begin{pmatrix}{{n}}\\{\mathrm{1}}\end{pmatrix}\begin{pmatrix}{{n}}\\{\mathrm{2}}\end{pmatrix}...\begin{pmatrix}{{n}}\\{{n}}\end{pmatrix}}\right) \\ $$

Question Number 42366 Answers: 1 Comments: 0

∫_(2005) ^(2017) (((ln ∣x − 2017∣)^(2017) )/((ln ∣x − 2015∣)^(2017) + (ln ∣x − 2017∣)^(2017) )) dx

$$\underset{\mathrm{2005}} {\overset{\mathrm{2017}} {\int}}\:\frac{\left(\mathrm{ln}\:\mid{x}\:−\:\mathrm{2017}\mid\right)^{\mathrm{2017}} }{\left(\mathrm{ln}\:\mid{x}\:−\:\mathrm{2015}\mid\right)^{\mathrm{2017}} \:+\:\left(\mathrm{ln}\:\mid{x}\:−\:\mathrm{2017}\mid\right)^{\mathrm{2017}} }\:{dx} \\ $$

Question Number 42364 Answers: 0 Comments: 3

∫ ((x + sinx − cosx − 1)/(x + e^x + sinx)) dx

$$\int\:\:\frac{\mathrm{x}\:+\:\mathrm{sinx}\:−\:\mathrm{cosx}\:−\:\mathrm{1}}{\mathrm{x}\:+\:\mathrm{e}^{\mathrm{x}} \:+\:\mathrm{sinx}}\:\mathrm{dx} \\ $$

Question Number 42401 Answers: 0 Comments: 1

calculate Σ_(n=0) ^∞ (((−1)^n )/((n+1)^2 ))

$${calculate}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }\: \\ $$

Question Number 42400 Answers: 0 Comments: 0

find lim_(n→+∞) (1/(√n)) Σ_(k=1) ^n (1/((√k) +(√(n−k))))

$${find}\:{lim}_{{n}\rightarrow+\infty} \:\frac{\mathrm{1}}{\sqrt{{n}}}\:\sum_{{k}=\mathrm{1}} ^{{n}} \:\:\frac{\mathrm{1}}{\sqrt{{k}}\:+\sqrt{{n}−{k}}} \\ $$

Question Number 42358 Answers: 1 Comments: 0

∫_( −1) ^( 1) (x^(2015) /(((1 + x))^(1/(2015)) + ((1 − x))^(1/(2015)) )) dx

$$\int_{\:−\mathrm{1}} ^{\:\mathrm{1}} \:\frac{\mathrm{x}^{\mathrm{2015}} }{\sqrt[{\mathrm{2015}}]{\mathrm{1}\:+\:\mathrm{x}}\:\:+\:\:\sqrt[{\mathrm{2015}}]{\mathrm{1}\:−\:\mathrm{x}}\:}\:\:\mathrm{dx} \\ $$

Question Number 42357 Answers: 1 Comments: 0

Question Number 42352 Answers: 1 Comments: 0

Question Number 42345 Answers: 1 Comments: 2

tan 15° =

$$\mathrm{tan}\:\mathrm{15}°\:= \\ $$

Question Number 42336 Answers: 0 Comments: 0

find ∫ ln(x−cosx)dx .

$${find}\:\:\int\:{ln}\left({x}−{cosx}\right){dx}\:. \\ $$

Question Number 42332 Answers: 0 Comments: 0

Question Number 42331 Answers: 1 Comments: 0

Question Number 42330 Answers: 0 Comments: 0

A linear function f(x)=ax + b transforms X={1,2,3,5,9,11} into Y,so that f(5)=13 and f(1)=5 Calculate the mean and Variance of X and Y.

$${A}\:{linear}\:{function}\:{f}\left({x}\right)={ax}\:+\:{b}\:{transforms}\:{X}=\left\{\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{5},\mathrm{9},\mathrm{11}\right\} \\ $$$${into}\:{Y},{so}\:{that}\:{f}\left(\mathrm{5}\right)=\mathrm{13}\:{and}\:{f}\left(\mathrm{1}\right)=\mathrm{5} \\ $$$${Calculate}\:{the}\:{mean}\:{and}\:{Variance}\:{of}\:{X}\:{and}\:{Y}. \\ $$

Question Number 42340 Answers: 2 Comments: 3

Question Number 42320 Answers: 1 Comments: 3

Question Number 42316 Answers: 1 Comments: 2

Question Number 42315 Answers: 2 Comments: 0

the point (2,−1) is reflected in the line x=4 find the image point.

$$\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{point}}\:\left(\mathrm{2},−\mathrm{1}\right)\:\boldsymbol{\mathrm{is}}\:\boldsymbol{\mathrm{reflected}}\: \\ $$$$\boldsymbol{\mathrm{in}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{line}}\:\:\boldsymbol{{x}}=\mathrm{4}\:\boldsymbol{\mathrm{find}}\:\boldsymbol{\mathrm{the}} \\ $$$$\boldsymbol{\mathrm{image}}\:\boldsymbol{\mathrm{point}}. \\ $$

Question Number 42314 Answers: 0 Comments: 1

Question Number 42528 Answers: 1 Comments: 0

Solve : ((p+2)/(2p+1)) = ((q+2p)/(2q+p)) = ((1+2q)/(2+q)) = λ. Find (p,q) ?

$$\mathrm{Solve}\:: \\ $$$$\frac{\mathrm{p}+\mathrm{2}}{\mathrm{2p}+\mathrm{1}}\:=\:\frac{\mathrm{q}+\mathrm{2p}}{\mathrm{2q}+\mathrm{p}}\:=\:\frac{\mathrm{1}+\mathrm{2q}}{\mathrm{2}+\mathrm{q}}\:=\:\lambda. \\ $$$$\mathrm{Find}\:\left(\mathrm{p},\mathrm{q}\right)\:? \\ $$

Question Number 42299 Answers: 1 Comments: 0

The set X and Y have five elementseach . Given that ΣX=25,ΣY=55,ΣX^2 =165 and ΣY^2 =765 and a linear Function y= px + q tranforms the set X into the set Y,where p and q are positive constants. a) Find the mean and Variance of X and Y hence,or otherwise , b)find the values of p and q.

$${The}\:{set}\:{X}\:{and}\:{Y}\:{have}\:{five}\:{elementseach}\:. \\ $$$${Given}\:{that}\:\Sigma{X}=\mathrm{25},\Sigma{Y}=\mathrm{55},\Sigma{X}^{\mathrm{2}} =\mathrm{165}\:{and}\:\Sigma{Y}^{\mathrm{2}} =\mathrm{765} \\ $$$${and}\:{a}\:{linear}\:{Function}\:{y}=\:{px}\:+\:{q}\:\:{tranforms}\:{the}\:{set}\:{X}\:{into}\:{the}\:{set}\: \\ $$$${Y},{where}\:{p}\:{and}\:{q}\:{are}\:{positive}\:{constants}. \\ $$$$\left.{a}\right)\:{Find}\:{the}\:{mean}\:{and}\:{Variance}\:{of}\:{X}\:{and}\:{Y} \\ $$$${hence},{or}\:{otherwise}\:, \\ $$$$\left.{b}\right){find}\:{the}\:{values}\:{of}\:{p}\:{and}\:{q}. \\ $$

Question Number 42296 Answers: 1 Comments: 1

solve in Z^2 2x+3y =7

$${solve}\:{in}\:{Z}^{\mathrm{2}} \:\:\:\:\:\:\:\mathrm{2}{x}+\mathrm{3}{y}\:=\mathrm{7} \\ $$

Question Number 42291 Answers: 1 Comments: 0

y = ((1080 − 19x)/(49)) (x,y ∈ Z) Find (x,y)

$${y}\:=\:\frac{\mathrm{1080}\:−\:\mathrm{19}{x}}{\mathrm{49}}\:\:\:\:\:\:\:\:\left({x},{y}\:\in\:\mathbb{Z}\right) \\ $$$$\mathrm{Find}\:\left({x},{y}\right) \\ $$

Pg 1659 Pg 1660 Pg 1661 Pg 1662 Pg 1663 Pg 1664 Pg 1665 Pg 1666 Pg 1667 Pg 1668

Contact: info@tinkutara.com