
AllQuestion and Answers: Page 1661
Question Number 43260 Answers: 0 Comments: 1
Question Number 43259 Answers: 0 Comments: 1
Question Number 43252 Answers: 3 Comments: 2

Question Number 43226 Answers: 1 Comments: 0
Question Number 43224 Answers: 1 Comments: 0
$${how}\:{many}\:{square}\:{in}\:{a}\:{chess}\:{board}. \\ $$
Question Number 43267 Answers: 0 Comments: 2
Question Number 43266 Answers: 1 Comments: 0
Question Number 43205 Answers: 1 Comments: 0

Question Number 43196 Answers: 0 Comments: 4

Question Number 43192 Answers: 1 Comments: 6

Question Number 43191 Answers: 1 Comments: 3
Question Number 43190 Answers: 1 Comments: 1
Question Number 43180 Answers: 1 Comments: 1
Question Number 43179 Answers: 1 Comments: 0
Question Number 43187 Answers: 2 Comments: 1
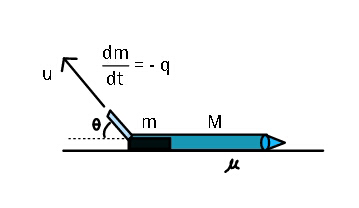
Question Number 43159 Answers: 1 Comments: 0

Question Number 43158 Answers: 2 Comments: 1
Question Number 43157 Answers: 1 Comments: 2
Question Number 43156 Answers: 1 Comments: 0
Question Number 43170 Answers: 1 Comments: 3
Question Number 43147 Answers: 0 Comments: 2
Question Number 43145 Answers: 1 Comments: 4
Question Number 43135 Answers: 1 Comments: 4
Question Number 43131 Answers: 2 Comments: 1

Question Number 43125 Answers: 1 Comments: 1

Question Number 43100 Answers: 1 Comments: 2
Pg 1656 Pg 1657 Pg 1658 Pg 1659 Pg 1660 Pg 1661 Pg 1662 Pg 1663 Pg 1664 Pg 1665
