
AllQuestion and Answers: Page 1660
Question Number 43365 Answers: 0 Comments: 0
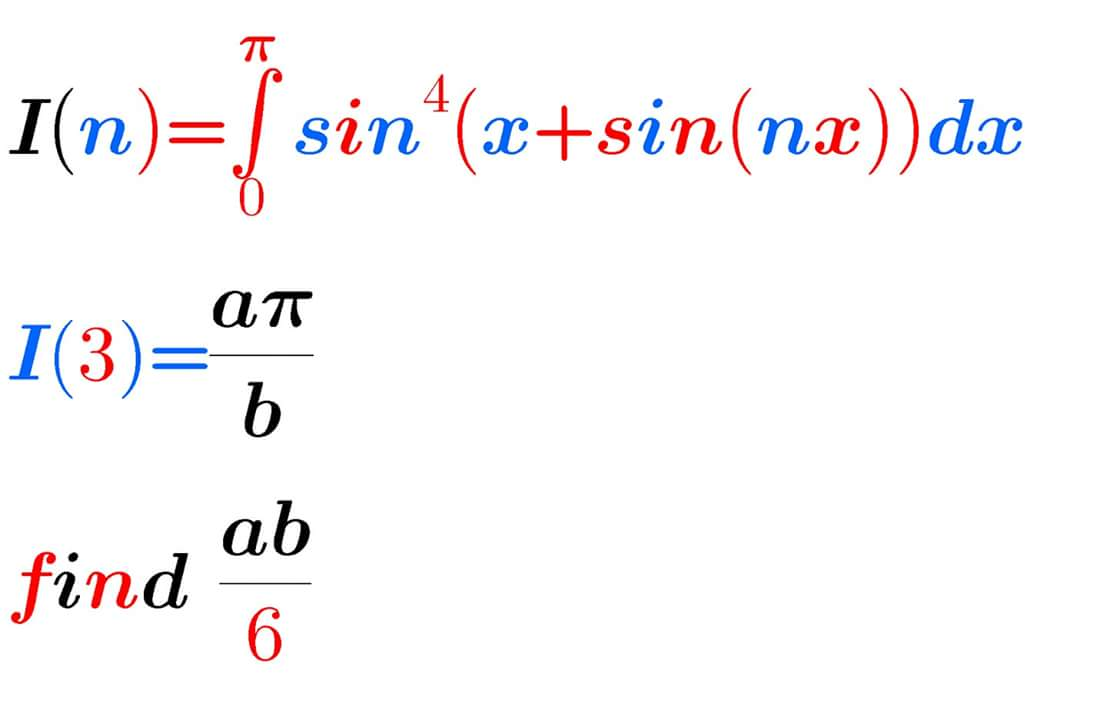
Question Number 43363 Answers: 3 Comments: 1
Question Number 43360 Answers: 0 Comments: 9

Question Number 43354 Answers: 1 Comments: 0
Question Number 43353 Answers: 2 Comments: 1
Question Number 43351 Answers: 0 Comments: 0

Question Number 43350 Answers: 1 Comments: 2

Question Number 43349 Answers: 2 Comments: 0

Question Number 43348 Answers: 1 Comments: 0

Question Number 43346 Answers: 1 Comments: 0
Question Number 43344 Answers: 0 Comments: 1
Question Number 43343 Answers: 1 Comments: 0
Question Number 43342 Answers: 1 Comments: 0
Question Number 43341 Answers: 1 Comments: 0
Question Number 43338 Answers: 1 Comments: 1
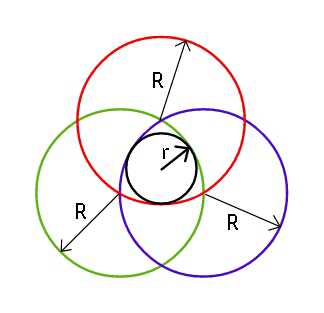
Question Number 43337 Answers: 0 Comments: 3
Question Number 43324 Answers: 1 Comments: 0

Question Number 43323 Answers: 0 Comments: 0

Question Number 43322 Answers: 1 Comments: 1

Question Number 43331 Answers: 0 Comments: 5

Question Number 43319 Answers: 1 Comments: 0
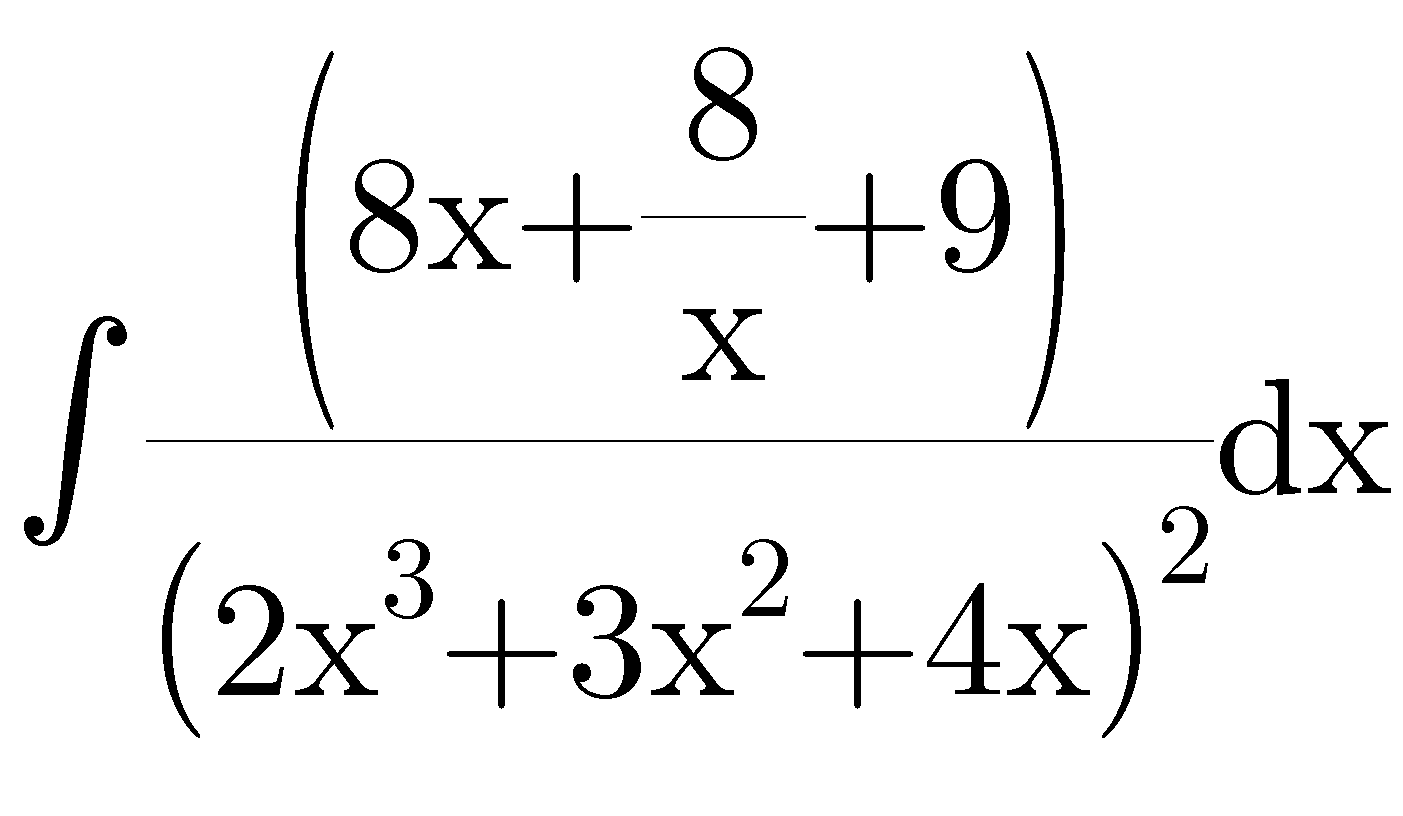
Question Number 43288 Answers: 0 Comments: 2

Question Number 43268 Answers: 0 Comments: 5
Question Number 43265 Answers: 0 Comments: 3

Question Number 43264 Answers: 2 Comments: 1

Question Number 43263 Answers: 2 Comments: 0

Pg 1655 Pg 1656 Pg 1657 Pg 1658 Pg 1659 Pg 1660 Pg 1661 Pg 1662 Pg 1663 Pg 1664
