
AllQuestion and Answers: Page 1659
Question Number 42994 Answers: 0 Comments: 5
$$\int\sqrt{\mathrm{1}+\frac{\mathrm{cos}\:{x}}{\mathrm{4tan}\:{x}}}{dx}=? \\ $$
Question Number 42988 Answers: 0 Comments: 0
Question Number 42948 Answers: 1 Comments: 5
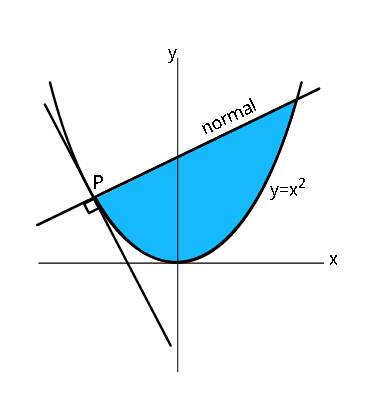
Question Number 42945 Answers: 2 Comments: 12
$$\int_{\mathrm{0}} ^{\:\:\pi/\mathrm{2}} \frac{{dx}}{\sqrt{\mathrm{sin}\:{x}}}\:=\:? \\ $$
Question Number 42942 Answers: 2 Comments: 0

Question Number 42934 Answers: 0 Comments: 2
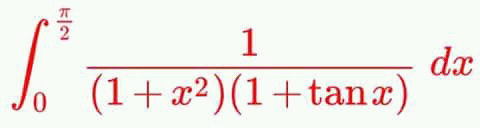
Question Number 42933 Answers: 0 Comments: 1
Question Number 42910 Answers: 1 Comments: 0
Question Number 42909 Answers: 1 Comments: 0
Question Number 42908 Answers: 1 Comments: 0
Question Number 42906 Answers: 3 Comments: 0
Question Number 42897 Answers: 2 Comments: 1
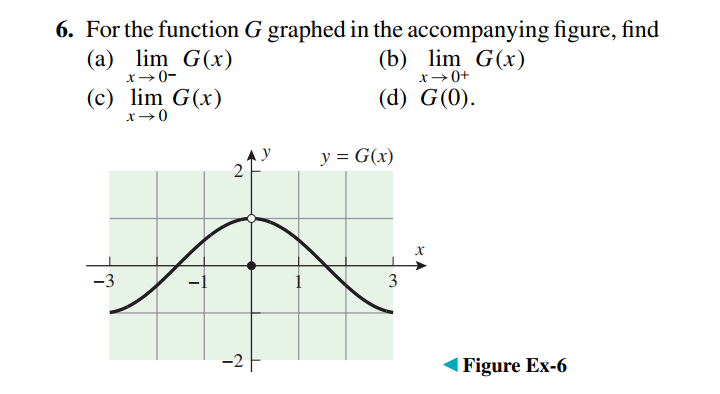
Question Number 42895 Answers: 1 Comments: 1
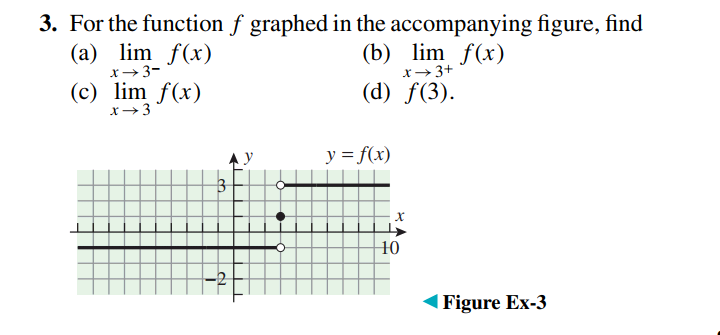
Question Number 42878 Answers: 1 Comments: 0
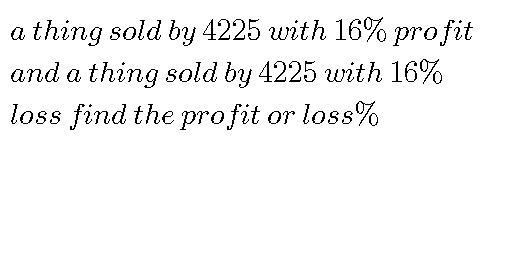
Question Number 42870 Answers: 0 Comments: 0
Question Number 42866 Answers: 2 Comments: 0

Question Number 42863 Answers: 2 Comments: 7

Question Number 42861 Answers: 1 Comments: 0
$$\mathrm{14}\boldsymbol{\div}\mathrm{2}\left(\mathrm{3}+\mathrm{4}\right)=? \\ $$
Question Number 42826 Answers: 0 Comments: 7
Question Number 42823 Answers: 1 Comments: 1
Question Number 42812 Answers: 0 Comments: 1
Question Number 42810 Answers: 1 Comments: 1
Question Number 42809 Answers: 1 Comments: 1
Question Number 42808 Answers: 1 Comments: 0
Question Number 42806 Answers: 0 Comments: 0
Question Number 42805 Answers: 1 Comments: 1
Pg 1654 Pg 1655 Pg 1656 Pg 1657 Pg 1658 Pg 1659 Pg 1660 Pg 1661 Pg 1662 Pg 1663
