
AllQuestion and Answers: Page 1658
Question Number 43596 Answers: 0 Comments: 0

Question Number 43574 Answers: 1 Comments: 0
Question Number 43571 Answers: 1 Comments: 0

Question Number 43569 Answers: 0 Comments: 1
Question Number 43551 Answers: 1 Comments: 0
Question Number 43550 Answers: 0 Comments: 1
Question Number 43549 Answers: 1 Comments: 1
Question Number 43546 Answers: 1 Comments: 0
Question Number 43545 Answers: 1 Comments: 0
Question Number 43544 Answers: 1 Comments: 0
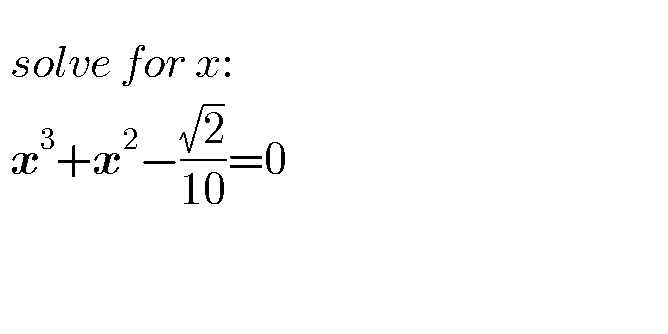
Question Number 43543 Answers: 1 Comments: 0
Question Number 43540 Answers: 2 Comments: 0
Question Number 43539 Answers: 0 Comments: 1
Question Number 43538 Answers: 0 Comments: 1
Question Number 43541 Answers: 1 Comments: 0
Question Number 43585 Answers: 2 Comments: 2

Question Number 43531 Answers: 1 Comments: 1
Question Number 43517 Answers: 0 Comments: 1

Question Number 43514 Answers: 0 Comments: 0
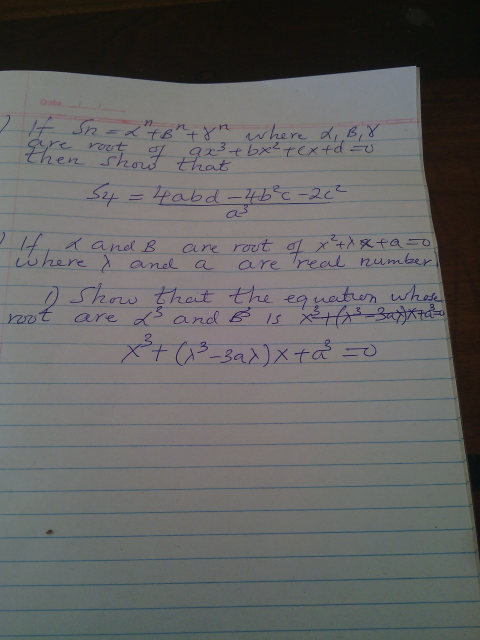
Question Number 43589 Answers: 1 Comments: 3

Question Number 43587 Answers: 1 Comments: 0
Question Number 43496 Answers: 1 Comments: 4
Question Number 43490 Answers: 1 Comments: 2
Question Number 43489 Answers: 1 Comments: 0
Question Number 43488 Answers: 1 Comments: 0
Question Number 43486 Answers: 3 Comments: 1

Pg 1653 Pg 1654 Pg 1655 Pg 1656 Pg 1657 Pg 1658 Pg 1659 Pg 1660 Pg 1661 Pg 1662
