Question and Answers Forum

AllQuestion and Answers: Page 1656

Question Number 43545 Answers: 1 Comments: 0

prove that ∫ _0 ^1 ((x^2 +6)/((x^2 +4)(x^2 +9)))=(Π/(20))

$${prove}\:{that}\:\int\:\underset{\mathrm{0}} {\overset{\mathrm{1}} {\:}}\:\frac{{x}^{\mathrm{2}} +\mathrm{6}}{\left({x}^{\mathrm{2}} +\mathrm{4}\right)\left({x}^{\mathrm{2}} +\mathrm{9}\right)}=\frac{\Pi}{\mathrm{20}} \\ $$

Question Number 43544 Answers: 1 Comments: 0

Question Number 43543 Answers: 1 Comments: 0

prove that (√(2+(√(2+(√(2+2cos 8θ)))))) 2cos θ

$${prove}\:{that}\:\:\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\mathrm{2cos}\:\mathrm{8}\theta}}} \\ $$$$\mathrm{2cos}\:\theta \\ $$

Question Number 43540 Answers: 2 Comments: 0

prove that 111 divide 10^(6n+2) +10^(3n+1) +1

$${prove}\:{that}\:\mathrm{111}\:{divide}\:\mathrm{10}^{\mathrm{6}{n}+\mathrm{2}} \:+\mathrm{10}^{\mathrm{3}{n}+\mathrm{1}} \:+\mathrm{1} \\ $$

Question Number 43539 Answers: 0 Comments: 1

calculate ∫∫_(0≤x≤1 ,0≤y≤1) (x+2y)e^(2x−y) dxdy

$${calculate}\:\int\int_{\mathrm{0}\leqslant{x}\leqslant\mathrm{1}\:,\mathrm{0}\leqslant{y}\leqslant\mathrm{1}} \:\:\left({x}+\mathrm{2}{y}\right){e}^{\mathrm{2}{x}−{y}} {dxdy} \\ $$

Question Number 43538 Answers: 0 Comments: 1

calculate ∫∫_((x^2 /a^2 ) +(y^2 /b^2 ) ≤1) (x^2 −y^2 )dxdy whit a>0 and b>0 .

$${calculate}\:\int\int_{\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\:+\frac{{y}^{\mathrm{2}} }{{b}^{\mathrm{2}} }\:\leqslant\mathrm{1}} \left({x}^{\mathrm{2}} −{y}^{\mathrm{2}} \right){dxdy}\:{whit} \\ $$$${a}>\mathrm{0}\:{and}\:{b}>\mathrm{0}\:. \\ $$

Question Number 43541 Answers: 1 Comments: 0

let u_0 =u_1 =1 and u_(n+1) =u_n +u_(n−1) 2) find u_n 3)let x_0 the positif roots of x^2 =x+1 4) prove that ∀n≥2 x_0 ^(n−2) ≤u_n ≤x_0 ^(n−1) .

$${let}\:{u}_{\mathrm{0}} ={u}_{\mathrm{1}} =\mathrm{1}\:{and}\:{u}_{{n}+\mathrm{1}} ={u}_{{n}} \:+{u}_{{n}−\mathrm{1}} \\ $$$$\left.\mathrm{2}\right)\:{find}\:{u}_{{n}} \\ $$$$\left.\mathrm{3}\right){let}\:{x}_{\mathrm{0}} \:\:{the}\:{positif}\:{roots}\:{of}\:{x}^{\mathrm{2}} ={x}+\mathrm{1} \\ $$$$\left.\mathrm{4}\right)\:{prove}\:{that}\:\forall{n}\geqslant\mathrm{2}\:\:{x}_{\mathrm{0}} ^{{n}−\mathrm{2}} \leqslant{u}_{{n}} \leqslant{x}_{\mathrm{0}} ^{{n}−\mathrm{1}} \:. \\ $$

Question Number 43585 Answers: 2 Comments: 2

Question Number 43531 Answers: 1 Comments: 1

the circumference of a circular track is 9 km. A cyclist rides round it a number of times and stops after covering a distance of 302 km. How far is the cyclist from the starting point? [take Π=((22)/7)]

$$\mathrm{the}\:\mathrm{circumference}\:\mathrm{of}\:\mathrm{a}\:\mathrm{circular}\:\mathrm{track}\:\mathrm{is}\:\mathrm{9}\:\mathrm{km}.\:\mathrm{A}\:\mathrm{cyclist} \\ $$$$\mathrm{rides}\:\mathrm{round}\:\mathrm{it}\:\mathrm{a}\:\mathrm{number}\:\mathrm{of}\:\mathrm{times}\:\mathrm{and}\:\mathrm{stops}\:\mathrm{after} \\ $$$$\mathrm{covering}\:\mathrm{a}\:\mathrm{distance}\:\mathrm{of}\:\mathrm{302}\:\mathrm{km}.\:\mathrm{How}\:\mathrm{far}\:\mathrm{is}\:\mathrm{the}\:\mathrm{cyclist} \\ $$$$\mathrm{from}\:\mathrm{the}\:\mathrm{starting}\:\mathrm{point}?\:\left[\mathrm{take}\:\Pi=\frac{\mathrm{22}}{\mathrm{7}}\right] \\ $$

Question Number 43517 Answers: 0 Comments: 1

Question Number 43514 Answers: 0 Comments: 0

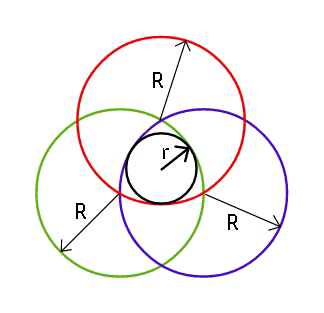
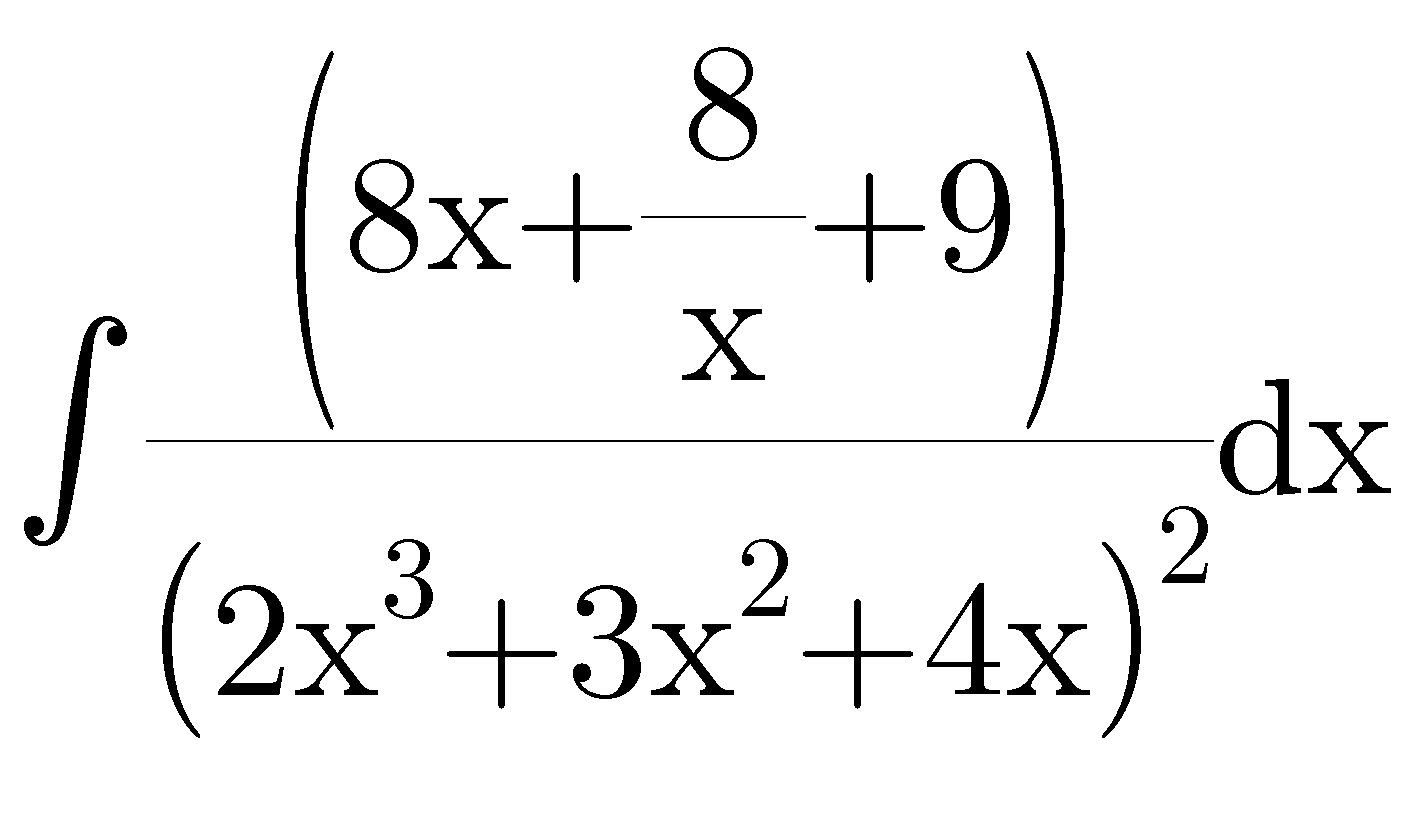
Question Number 43589 Answers: 1 Comments: 3

Question Number 43587 Answers: 1 Comments: 0

a and b are the digit in a four digit number 12ab.if 12ab is divisble by 5 and 9 .find the sum of all possible value of a.

$${a}\:{and}\:{b}\:\:{are}\:{the}\:{digit}\:{in}\:{a}\:{four}\:{digit} \\ $$$${number}\:\mathrm{12}{ab}.{if}\:\mathrm{12}{ab}\:{is}\:{divisble}\:{by}\: \\ $$$$\mathrm{5}\:{and}\:\mathrm{9}\:.{find}\:{the}\:{sum}\:{of}\:{all}\:{possible} \\ $$$${value}\:{of}\:\:{a}. \\ $$

Question Number 43496 Answers: 1 Comments: 4

(√(a−(√(a+x)))) + (√(a+(√(a−x)))) =2x Solve for “ x ” in terms of “ a ”

$$\sqrt{\mathrm{a}−\sqrt{\mathrm{a}+\mathrm{x}}}\:\:+\:\:\sqrt{\mathrm{a}+\sqrt{\mathrm{a}−\mathrm{x}}}\:\:=\mathrm{2x}\: \\ $$$$\mathrm{Solve}\:\mathrm{for}\:``\:\mathrm{x}\:''\:\mathrm{in}\:\mathrm{terms}\:\mathrm{of}\:\:``\:\:\mathrm{a}\:\:'' \\ $$$$ \\ $$

Question Number 43490 Answers: 1 Comments: 2

evaluate ∫(√(tan𝛉 dθ))

$$\boldsymbol{\mathrm{evaluate}} \\ $$$$\int\sqrt{\boldsymbol{\mathrm{tan}\theta}\:\boldsymbol{\mathrm{d}}\theta} \\ $$

Question Number 43489 Answers: 1 Comments: 0

if y=cos(logx) +3sin(logx) prove that x^2 (d^2 x/dx^2 )+x(dy/dx)+y=0

$${if}\:{y}={cos}\left({logx}\right)\:+\mathrm{3}{sin}\left({logx}\right)\:{prove}\:{that} \\ $$$${x}^{\mathrm{2}} \:\frac{{d}^{\mathrm{2}} {x}}{{dx}^{\mathrm{2}} }+{x}\frac{{dy}}{{dx}}+{y}=\mathrm{0} \\ $$

Question Number 43488 Answers: 1 Comments: 0

if the root of x^3 +px_ ^2 +qx+30=0 are in the ratio 2:3:5find the value of p and q

$${if}\:{the}\:{root}\:{of}\:\:{x}^{\mathrm{3}} +{px}_{} ^{\mathrm{2}} +{qx}+\mathrm{30}=\mathrm{0}\:{are} \\ $$$${in}\:{the}\:{ratio}\:\mathrm{2}:\mathrm{3}:\mathrm{5}{find}\:{the}\:{value}\:{of}\:{p}\:{and}\:{q} \\ $$

Question Number 43486 Answers: 3 Comments: 1

Question Number 43481 Answers: 1 Comments: 0

(((1+2i)^3 )/((3+i)))=

$$\frac{\left(\mathrm{1}+\mathrm{2}{i}\right)^{\mathrm{3}} }{\left(\mathrm{3}+{i}\right)}= \\ $$

Question Number 43471 Answers: 1 Comments: 0

Question Number 43470 Answers: 0 Comments: 0

Please what topic is all the question that has the summation sign. Σ. How can i study the summation by using it to solve some continuous equation.

$$\mathrm{Please}\:\mathrm{what}\:\mathrm{topic}\:\mathrm{is}\:\mathrm{all}\:\mathrm{the}\:\mathrm{question}\:\mathrm{that}\:\mathrm{has}\:\mathrm{the}\:\mathrm{summation}\:\mathrm{sign}. \\ $$$$\Sigma.\:\:\:\:\mathrm{How}\:\mathrm{can}\:\mathrm{i}\:\mathrm{study}\:\mathrm{the}\:\mathrm{summation}\:\mathrm{by}\:\mathrm{using}\:\mathrm{it}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{some}\:\mathrm{continuous} \\ $$$$\mathrm{equation}. \\ $$

Question Number 43467 Answers: 2 Comments: 0

prove that tanθ+2tan2θ+4tan 4θ +8cot8θ=cotθ

$${prove}\:{th}\mathrm{at}\:\mathrm{tan}\theta+\mathrm{2}{tan}\mathrm{2}\theta+\mathrm{4}{tan}\:\:\:\mathrm{4}\theta \\ $$$$+\mathrm{8cot8}\theta={cot}\theta \\ $$

Question Number 43465 Answers: 2 Comments: 1

Question Number 43463 Answers: 0 Comments: 1

Question Number 43461 Answers: 0 Comments: 1

found something (others have found before) which I thought might be of interest, especially for Sir Tanmay Chaudhury: take any polynome of degree 4 with 2 real inflection points y=ax^4 +bx^3 +cx^2 +dx+e y′′=12ax^2 +6bx+2c=0 has got 2 real solutions x_1 and x_2 the line connecting the inflection points intersects the curve in 2 more points P and Q, their x−values are p and q let p<x_1 <x_2 <q ⇒ ((x_2 −x_1 )/(x_1 −p))=((x_2 −x_1 )/(q−x_2 ))=(1/2)+((√5)/2) which is the Golden Ratio

$$\mathrm{found}\:\mathrm{something}\:\left(\mathrm{others}\:\mathrm{have}\:\mathrm{found}\:\mathrm{before}\right) \\ $$$$\mathrm{which}\:\mathrm{I}\:\mathrm{thought}\:\mathrm{might}\:\mathrm{be}\:\mathrm{of}\:\mathrm{interest}, \\ $$$$\mathrm{especially}\:\mathrm{for}\:\mathrm{Sir}\:\mathrm{Tanmay}\:\mathrm{Chaudhury}: \\ $$$$\mathrm{take}\:\mathrm{any}\:\mathrm{polynome}\:\mathrm{of}\:\mathrm{degree}\:\mathrm{4}\:\mathrm{with}\:\mathrm{2}\:\mathrm{real} \\ $$$$\mathrm{inflection}\:\mathrm{points} \\ $$$${y}={ax}^{\mathrm{4}} +{bx}^{\mathrm{3}} +{cx}^{\mathrm{2}} +{dx}+{e} \\ $$$${y}''=\mathrm{12}{ax}^{\mathrm{2}} +\mathrm{6}{bx}+\mathrm{2}{c}=\mathrm{0}\:\mathrm{has}\:\mathrm{got}\:\mathrm{2}\:\mathrm{real}\:\mathrm{solutions} \\ $$$${x}_{\mathrm{1}} \:\mathrm{and}\:{x}_{\mathrm{2}} \\ $$$$\mathrm{the}\:\mathrm{line}\:\mathrm{connecting}\:\mathrm{the}\:\mathrm{inflection}\:\mathrm{points} \\ $$$$\mathrm{intersects}\:\mathrm{the}\:\mathrm{curve}\:\mathrm{in}\:\mathrm{2}\:\mathrm{more}\:\mathrm{points} \\ $$$${P}\:\mathrm{and}\:{Q},\:\mathrm{their}\:{x}−\mathrm{values}\:\mathrm{are}\:{p}\:\mathrm{and}\:{q} \\ $$$$\mathrm{let}\:{p}<{x}_{\mathrm{1}} <{x}_{\mathrm{2}} <{q} \\ $$$$\Rightarrow\:\frac{{x}_{\mathrm{2}} −{x}_{\mathrm{1}} }{{x}_{\mathrm{1}} −{p}}=\frac{{x}_{\mathrm{2}} −{x}_{\mathrm{1}} }{{q}−{x}_{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\:\mathrm{which}\:\mathrm{is}\:\mathrm{the}\:\mathrm{Golden}\:\mathrm{Ratio} \\ $$

Question Number 43454 Answers: 0 Comments: 0

qn: There is a group of 50 people who are patriotic out of which 20 believes in non violence. Two persons are selected at rondom out of them. write the probability distribution for the selected persons who are non violent. also find the mean of the distribution. explain the importance of non violence in patriotism.

$$\mathrm{qn}:\:\mathrm{There}\:\mathrm{is}\:\mathrm{a}\:\mathrm{group}\:\mathrm{of}\:\mathrm{50}\:\mathrm{people} \\ $$$$\mathrm{who}\:\mathrm{are}\:\mathrm{patriotic}\:\mathrm{out}\:\mathrm{of}\:\mathrm{which}\:\mathrm{20} \\ $$$$\mathrm{believes}\:\mathrm{in}\:\mathrm{non}\:\mathrm{violence}.\:\mathrm{Two}\:\mathrm{persons} \\ $$$$\mathrm{are}\:\mathrm{selected}\:\mathrm{at}\:\mathrm{rondom}\:\mathrm{out}\:\mathrm{of}\:\mathrm{them}. \\ $$$$\mathrm{write}\:\mathrm{the}\:\mathrm{probability}\:\mathrm{distribution}\:\mathrm{for}\:\mathrm{the} \\ $$$$\mathrm{selected}\:\mathrm{persons}\:\mathrm{who}\:\mathrm{are}\:\mathrm{non}\:\mathrm{violent}. \\ $$$$\mathrm{also}\:\mathrm{find}\:\mathrm{the}\:\mathrm{mean}\:\mathrm{of}\:\mathrm{the}\:\mathrm{distribution}. \\ $$$$\mathrm{explain}\:\mathrm{the}\:\mathrm{importance}\:\mathrm{of}\:\mathrm{non}\:\mathrm{violence}\:\mathrm{in}\:\mathrm{patriotism}. \\ $$$$ \\ $$$$ \\ $$

Pg 1651 Pg 1652 Pg 1653 Pg 1654 Pg 1655 Pg 1656 Pg 1657 Pg 1658 Pg 1659 Pg 1660

Contact: info@tinkutara.com