
AllQuestion and Answers: Page 1637
Question Number 46024 Answers: 0 Comments: 1
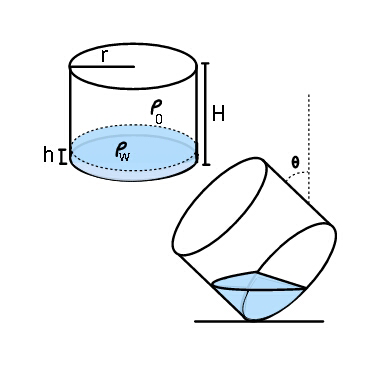
Question Number 46007 Answers: 1 Comments: 0

Question Number 46003 Answers: 1 Comments: 1

Question Number 45994 Answers: 2 Comments: 0

Question Number 45993 Answers: 1 Comments: 1

Question Number 45992 Answers: 1 Comments: 0

Question Number 45982 Answers: 1 Comments: 1
Question Number 45980 Answers: 1 Comments: 1

Question Number 45976 Answers: 0 Comments: 1
Question Number 45975 Answers: 0 Comments: 0
Question Number 45974 Answers: 0 Comments: 0
Question Number 45973 Answers: 0 Comments: 0
Question Number 45972 Answers: 0 Comments: 0
Question Number 45971 Answers: 0 Comments: 0
Question Number 45970 Answers: 1 Comments: 1
Question Number 45968 Answers: 1 Comments: 2
Question Number 45969 Answers: 0 Comments: 0
Question Number 45961 Answers: 0 Comments: 0
Question Number 45960 Answers: 1 Comments: 0
Question Number 45957 Answers: 1 Comments: 1
Question Number 45962 Answers: 0 Comments: 0
Question Number 45963 Answers: 1 Comments: 1
Question Number 45941 Answers: 1 Comments: 0
Question Number 45936 Answers: 0 Comments: 1

Question Number 45932 Answers: 1 Comments: 4
Question Number 45931 Answers: 0 Comments: 0

Pg 1632 Pg 1633 Pg 1634 Pg 1635 Pg 1636 Pg 1637 Pg 1638 Pg 1639 Pg 1640 Pg 1641
