Question and Answers Forum

AllQuestion and Answers: Page 1634

Question Number 44674 Answers: 0 Comments: 1

solving some integrals we might meet some of the following functions which cannot be solved with elementar knowledge but tables should exist somewhere in the depth of the www... these links might be interesting exponential integral ∫(e^(−x) /x)dx en.wikipedia.org/wiki/Exponential_integral logarithmic integral ∫(dx/(ln x)) en.wikipedia.org/wiki/Logarithmic_integral_function also see en.wikipedia.org/wiki/Polylogarithm trigonometric integrals i.e. ∫((sin x)/x)dx en.wikipedia.org/wiki/Trigonometric_integral

$$\mathrm{solving}\:\mathrm{some}\:\mathrm{integrals}\:\mathrm{we}\:\mathrm{might}\:\mathrm{meet}\:\mathrm{some} \\ $$$$\mathrm{of}\:\mathrm{the}\:\mathrm{following}\:\mathrm{functions}\:\mathrm{which}\:\mathrm{cannot}\:\mathrm{be} \\ $$$$\mathrm{solved}\:\mathrm{with}\:\mathrm{elementar}\:\mathrm{knowledge}\:\mathrm{but}\:\mathrm{tables} \\ $$$$\mathrm{should}\:\mathrm{exist}\:\mathrm{somewhere}\:\mathrm{in}\:\mathrm{the}\:\mathrm{depth}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{www}... \\ $$$$\mathrm{these}\:\mathrm{links}\:\mathrm{might}\:\mathrm{be}\:\mathrm{interesting} \\ $$$$ \\ $$$$\mathrm{exponential}\:\mathrm{integral} \\ $$$$\int\frac{\mathrm{e}^{−{x}} }{{x}}{dx} \\ $$$$\mathrm{en}.\mathrm{wikipedia}.\mathrm{org}/\mathrm{wiki}/\mathrm{Exponential\_integral} \\ $$$$ \\ $$$$\mathrm{logarithmic}\:\mathrm{integral} \\ $$$$\int\frac{{dx}}{\mathrm{ln}\:{x}} \\ $$$$\mathrm{en}.\mathrm{wikipedia}.\mathrm{org}/\mathrm{wiki}/\mathrm{Logarithmic\_integral\_function} \\ $$$$\mathrm{also}\:\mathrm{see} \\ $$$$\mathrm{en}.\mathrm{wikipedia}.\mathrm{org}/\mathrm{wiki}/\mathrm{Polylogarithm} \\ $$$$ \\ $$$$\mathrm{trigonometric}\:\mathrm{integrals} \\ $$$$\mathrm{i}.\mathrm{e}.\:\int\frac{\mathrm{sin}\:{x}}{{x}}{dx} \\ $$$$\mathrm{en}.\mathrm{wikipedia}.\mathrm{org}/\mathrm{wiki}/\mathrm{Trigonometric\_integral} \\ $$

Question Number 44570 Answers: 1 Comments: 0

Question Number 44573 Answers: 1 Comments: 1

Question Number 44575 Answers: 1 Comments: 3

Question Number 44557 Answers: 1 Comments: 2

Question Number 44548 Answers: 0 Comments: 0

(a) The area of a sector of a circle of radius 12cm is 132cm^2 . If the sector is folded such that its straight edges coincide to form a cone. Find the radius of the base of the cone [ Take π = ((22)/7) ] . (b) A circle of centre O has radius 5cm. A chord PQ of the circle is 6cm long. caclculate: (i) The distance of the chord from the centre O (ii) The angle POQ

$$\left(\mathrm{a}\right) \\ $$$$\mathrm{The}\:\mathrm{area}\:\mathrm{of}\:\mathrm{a}\:\mathrm{sector}\:\mathrm{of}\:\mathrm{a}\:\mathrm{circle}\:\mathrm{of}\:\mathrm{radius}\:\:\mathrm{12cm}\:\mathrm{is}\:\:\mathrm{132cm}^{\mathrm{2}} \:.\:\:\mathrm{If}\:\mathrm{the}\:\mathrm{sector} \\ $$$$\mathrm{is}\:\mathrm{folded}\:\mathrm{such}\:\mathrm{that}\:\mathrm{its}\:\mathrm{straight}\:\mathrm{edges}\:\mathrm{coincide}\:\mathrm{to}\:\mathrm{form}\:\mathrm{a}\:\mathrm{cone}.\:\mathrm{Find}\:\mathrm{the}\: \\ $$$$\mathrm{radius}\:\mathrm{of}\:\mathrm{the}\:\mathrm{base}\:\mathrm{of}\:\mathrm{the}\:\mathrm{cone}\:\:\:\:\left[\:\:\mathrm{Take}\:\:\:\:\pi\:\:=\:\:\frac{\mathrm{22}}{\mathrm{7}}\:\right]\:. \\ $$$$ \\ $$$$\left(\mathrm{b}\right)\:\:\: \\ $$$$\mathrm{A}\:\mathrm{circle}\:\mathrm{of}\:\mathrm{centre}\:\mathrm{O}\:\mathrm{has}\:\mathrm{radius}\:\mathrm{5cm}.\:\:\mathrm{A}\:\mathrm{chord}\:\mathrm{PQ}\:\mathrm{of}\:\mathrm{the}\:\mathrm{circle}\:\mathrm{is}\:\mathrm{6cm}\:\mathrm{long}. \\ $$$$\mathrm{caclculate}: \\ $$$$\:\:\:\:\left(\mathrm{i}\right)\:\:\:\mathrm{The}\:\mathrm{distance}\:\mathrm{of}\:\mathrm{the}\:\mathrm{chord}\:\mathrm{from}\:\mathrm{the}\:\mathrm{centre}\:\mathrm{O} \\ $$$$\:\:\:\left(\mathrm{ii}\right)\:\:\mathrm{The}\:\mathrm{angle}\:\mathrm{POQ} \\ $$

Question Number 44546 Answers: 1 Comments: 0

$$ \\ $$

Question Number 44543 Answers: 1 Comments: 3

If y =f(x) = ax^2 +bx+c and at some x, say x= p ∫_0 ^( p) ydx = y(p)= y ′(p) = y ′′(p)= p , then find p .

$${If}\:\:{y}\:={f}\left({x}\right)\:=\:{ax}^{\mathrm{2}} +{bx}+{c} \\ $$$${and}\:\:{at}\:{some}\:{x},\:{say}\:\:{x}=\:{p} \\ $$$$\int_{\mathrm{0}} ^{\:\:{p}} {ydx}\:=\:{y}\left({p}\right)=\:{y}\:'\left({p}\right)\:=\:{y}\:''\left({p}\right)=\:{p}\:, \\ $$$${then}\:{find}\:\boldsymbol{{p}}\:. \\ $$

Question Number 44541 Answers: 1 Comments: 1

Find the remainder when the polynomial p(y)=y^4 −3y^2 +2y+1 is divided by y−1.

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{remainder}\:\mathrm{when}\:\mathrm{the} \\ $$$$\mathrm{polynomial}\:{p}\left({y}\right)={y}^{\mathrm{4}} −\mathrm{3}{y}^{\mathrm{2}} +\mathrm{2}{y}+\mathrm{1}\:\mathrm{is} \\ $$$$\mathrm{divided}\:\mathrm{by}\:{y}−\mathrm{1}. \\ $$

Question Number 44537 Answers: 1 Comments: 0

Question Number 44535 Answers: 0 Comments: 1

Question Number 44527 Answers: 0 Comments: 2

Question Number 44526 Answers: 1 Comments: 1

Find moment of inertia of the area bounded by the curve r^2 =a^2 cos2θ about its axis

$$\mathrm{Find}\:\mathrm{moment}\:\mathrm{of}\:\mathrm{inertia}\:\mathrm{of}\:\mathrm{the}\:\mathrm{area}\:\mathrm{bounded} \\ $$$$\mathrm{by}\:\mathrm{the}\:\mathrm{curve}\:\mathrm{r}^{\mathrm{2}} =\mathrm{a}^{\mathrm{2}} \mathrm{cos2}\theta \\ $$$$\mathrm{about}\:\mathrm{its}\:\mathrm{axis} \\ $$

Question Number 44515 Answers: 1 Comments: 0

let g(x) =∫_0 ^∞ ((t ln(t)dt)/((1+xt)^3 )) with x>0 1) give a explicit form of g(x) 2) calculate ∫_0 ^∞ ((t ln(t))/((1+t)^3 ))dt 3) calculate ∫_0 ^∞ ((tln(t))/((1+2t)^3 )) dt 4) calculate A(θ) =∫_0 ^∞ ((t ln(t))/((1+t sinθ)^3 ))dt with 0<θ<(π/2)

$${let}\:{g}\left({x}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{t}\:{ln}\left({t}\right){dt}}{\left(\mathrm{1}+{xt}\right)^{\mathrm{3}} }\:{with}\:{x}>\mathrm{0} \\ $$$$\left.\mathrm{1}\right)\:{give}\:{a}\:{explicit}\:{form}\:{of}\:{g}\left({x}\right) \\ $$$$\left.\mathrm{2}\right)\:{calculate}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{t}\:{ln}\left({t}\right)}{\left(\mathrm{1}+{t}\right)^{\mathrm{3}} }{dt} \\ $$$$\left.\mathrm{3}\right)\:{calculate}\:\int_{\mathrm{0}} ^{\infty} \:\frac{{tln}\left({t}\right)}{\left(\mathrm{1}+\mathrm{2}{t}\right)^{\mathrm{3}} }\:{dt} \\ $$$$\left.\mathrm{4}\right)\:{calculate}\:{A}\left(\theta\right)\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{t}\:{ln}\left({t}\right)}{\left(\mathrm{1}+{t}\:{sin}\theta\right)^{\mathrm{3}} }{dt}\:\:{with}\:\:\mathrm{0}<\theta<\frac{\pi}{\mathrm{2}} \\ $$

Question Number 44512 Answers: 1 Comments: 1

prove that:−∫2^(ln x) dx = ((x.2^(ln x) )/(ln(xe))) +C

$$\boldsymbol{{prove}}\:\boldsymbol{{that}}:−\int\mathrm{2}^{\boldsymbol{\mathrm{ln}}\:\boldsymbol{\mathrm{x}}} \:\boldsymbol{\mathrm{dx}}\:=\:\frac{\boldsymbol{\mathrm{x}}.\mathrm{2}^{\boldsymbol{\mathrm{ln}}\:\boldsymbol{\mathrm{x}}} }{\boldsymbol{\mathrm{ln}}\left(\boldsymbol{\mathrm{xe}}\right)}\:+\boldsymbol{\mathrm{C}} \\ $$$$ \\ $$

Question Number 44509 Answers: 1 Comments: 1

∫(√(tan x)) dx=?

$$\int\sqrt{\boldsymbol{\mathrm{tan}}\:\boldsymbol{\mathrm{x}}}\:\:\boldsymbol{\mathrm{dx}}=? \\ $$

Question Number 44508 Answers: 1 Comments: 1

∫(√(sin x ))dx=?

$$\int\sqrt{\boldsymbol{\mathrm{sin}}\:\boldsymbol{\mathrm{x}}\:}\boldsymbol{\mathrm{dx}}=? \\ $$

Question Number 44502 Answers: 1 Comments: 0

If a>b,and c>d,prove that a−c may be greater than, equal to or less than b−d.

$$\mathrm{If}\:\mathrm{a}>\mathrm{b},\mathrm{and}\:\mathrm{c}>\mathrm{d},\mathrm{prove}\:\mathrm{that}\:\mathrm{a}−\mathrm{c}\:\mathrm{may}\:\mathrm{be}\:\mathrm{greater}\:\mathrm{than}, \\ $$$$\mathrm{equal}\:\mathrm{to}\:\mathrm{or}\:\mathrm{less}\:\mathrm{than}\:\mathrm{b}−\mathrm{d}. \\ $$$$ \\ $$

Question Number 44498 Answers: 0 Comments: 2

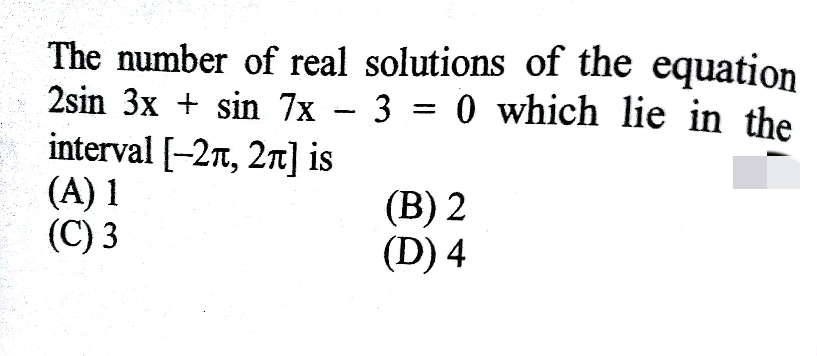
Question Number 44497 Answers: 0 Comments: 8

Question Number 44480 Answers: 2 Comments: 0

prove that ((9π)/(8 ))−(9/4)sin^(−1) (1/3)=(9/4)sin^(−1) ((2(√2))/3)

$${prove}\:{that}\:\:\frac{\mathrm{9}\pi}{\mathrm{8}\:\:}−\frac{\mathrm{9}}{\mathrm{4}}\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{3}}=\frac{\mathrm{9}}{\mathrm{4}}\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}} \\ $$

Question Number 44479 Answers: 1 Comments: 5

Question Number 44478 Answers: 1 Comments: 0

prove that 2tan^(−1) ((√((a−b)/(a+b ))) tan (θ/2))=cos^(−1) (((b+acosθ)/(a+bcosθ)))

$${prove}\:{that}\:\mathrm{2tan}^{−\mathrm{1}} \left(\sqrt{\frac{{a}−{b}}{{a}+{b}\:}}\:\:\mathrm{tan}\:\frac{\theta}{\mathrm{2}}\right)=\mathrm{cos}^{−\mathrm{1}} \left(\frac{{b}+{acos}\theta}{{a}+{bcos}\theta}\right) \\ $$

Question Number 44491 Answers: 1 Comments: 0

prove that the sum of interior angles of any triangle is 180.

$$\boldsymbol{\mathrm{prove}}\:\boldsymbol{\mathrm{that}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{sum}}\:\boldsymbol{\mathrm{of}}\:\boldsymbol{\mathrm{interior}}\:\boldsymbol{\mathrm{angles}} \\ $$$$\boldsymbol{\mathrm{of}}\:\boldsymbol{\mathrm{any}}\:\boldsymbol{\mathrm{triangle}}\:\boldsymbol{\mathrm{is}}\:\mathrm{180}. \\ $$

Question Number 44476 Answers: 0 Comments: 6

let f(x) =∫_0 ^∞ (dt/(t^2 +2xt−1)) 1)find a explicit form of f(x) 2) cslvulste ∫_0 ^∞ (dt/(t^2 +t−1)) 3)calculate A(θ)=∫_0 ^∞ (dt/(t^2 +2tan(θ)t −1)) 4) calculate g(x)=∫_0 ^∞ ((tdt)/((t^2 +2xt−1)^2 )) 5)find the value of ∫_0 ^∞ ((tdt)/((t^2 +4t−1)^2 ))

$${let}\:{f}\left({x}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{{dt}}{{t}^{\mathrm{2}} \:+\mathrm{2}{xt}−\mathrm{1}} \\ $$$$\left.\mathrm{1}\right){find}\:{a}\:{explicit}\:{form}\:{of}\:{f}\left({x}\right) \\ $$$$\left.\mathrm{2}\right)\:{cslvulste}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{{dt}}{{t}^{\mathrm{2}} \:+{t}−\mathrm{1}} \\ $$$$\left.\mathrm{3}\right){calculate}\:{A}\left(\theta\right)=\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{dt}}{{t}^{\mathrm{2}} \:+\mathrm{2}{tan}\left(\theta\right){t}\:−\mathrm{1}} \\ $$$$\left.\mathrm{4}\right)\:{calculate}\:{g}\left({x}\right)=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{tdt}}{\left({t}^{\mathrm{2}} \:+\mathrm{2}{xt}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\left.\mathrm{5}\right){find}\:{the}\:{value}\:{of}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{{tdt}}{\left({t}^{\mathrm{2}} \:+\mathrm{4}{t}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$

Question Number 44475 Answers: 0 Comments: 0

find a and b if ∫_0 ^∞ ((√t) +a(√(t+1))+b(√(t+2)))dt converges and give its value in this case.

$${find}\:{a}\:{and}\:{b}\:\:{if}\:\int_{\mathrm{0}} ^{\infty} \:\left(\sqrt{{t}}\:+{a}\sqrt{{t}+\mathrm{1}}+{b}\sqrt{{t}+\mathrm{2}}\right){dt} \\ $$$${converges}\:{and}\:{give}\:{its}\:{value}\:{in}\:{this}\:{case}. \\ $$

Pg 1629 Pg 1630 Pg 1631 Pg 1632 Pg 1633 Pg 1634 Pg 1635 Pg 1636 Pg 1637 Pg 1638

Contact: info@tinkutara.com