Question and Answers Forum

AllQuestion and Answers: Page 1631

Question Number 36080 Answers: 2 Comments: 1

i want to know how α^2 + β^2 = (α+β)^2 − 2αβ why not α^2 +β^2 = (α+β)^2 + 2αβ?

$$\:\mathrm{i}\:\mathrm{want}\:\mathrm{to}\:\mathrm{know}\:\mathrm{how}\: \\ $$$$\alpha^{\mathrm{2}} +\:\beta^{\mathrm{2}} =\:\left(\alpha+\beta\right)^{\mathrm{2}} −\:\mathrm{2}\alpha\beta\:\mathrm{why}\:\mathrm{not}\: \\ $$$$\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} =\:\left(\alpha+\beta\right)^{\mathrm{2}} +\:\mathrm{2}\alpha\beta? \\ $$

Question Number 36068 Answers: 0 Comments: 1

Why is it not advisable to use small incident angle when performing experiment on refraction using a triangular prism?

$${Why}\:{is}\:{it}\:{not}\:{advisable}\:{to}\:{use} \\ $$$${small}\:{incident}\:{angle}\:{when}\:{performing} \\ $$$${experiment}\:{on}\:{refraction}\:{using}\:{a} \\ $$$${triangular}\:{prism}? \\ $$

Question Number 36061 Answers: 1 Comments: 2

Question Number 36059 Answers: 1 Comments: 0

Question Number 36057 Answers: 2 Comments: 1

find the value of ∫_0 ^(π/4) ((cosx)/(sinx +tanx))dx

$${find}\:{the}\:{value}\:{of}\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\:\:\frac{{cosx}}{{sinx}\:+{tanx}}{dx}\: \\ $$

Question Number 36056 Answers: 1 Comments: 2

calculate ∫_(−∞) ^(+∞) ((2x)/((x^2 +mx +1)^2 ))dx with ∣m∣<2

$${calculate}\:\:\int_{−\infty} ^{+\infty} \:\:\:\frac{\mathrm{2}{x}}{\left({x}^{\mathrm{2}} \:+{mx}\:+\mathrm{1}\right)^{\mathrm{2}} }{dx}\:{with}\:\mid{m}\mid<\mathrm{2} \\ $$

Question Number 36049 Answers: 0 Comments: 0

A triangle △ABC is constructed such that ∠B= 90° and AB= 5cm Given that ∠C= 45° . show that the point (2,0) lie on the line BC and is perpendicular to AB but meet at 45^ ° with the line AC.

$$\mathrm{A}\:\mathrm{triangle}\:\bigtriangleup\mathrm{ABC}\:\mathrm{is}\:\mathrm{constructed}\: \\ $$$$\mathrm{such}\:\mathrm{that}\:\angle\mathrm{B}=\:\mathrm{90}°\:\:\mathrm{and}\:\mathrm{AB}=\:\mathrm{5cm} \\ $$$$\mathrm{Given}\:\mathrm{that}\:\angle\mathrm{C}=\:\mathrm{45}°\:.\:\mathrm{show}\:\mathrm{that} \\ $$$$\:\mathrm{the}\:\mathrm{point}\:\left(\mathrm{2},\mathrm{0}\right)\:\mathrm{lie}\:\mathrm{on}\:\mathrm{the}\:\mathrm{line}\: \\ $$$$\mathrm{BC}\:\mathrm{and}\:\mathrm{is}\:\mathrm{perpendicular}\:\mathrm{to}\:\mathrm{AB}\:\mathrm{but} \\ $$$$\mathrm{meet}\:\mathrm{at}\:\mathrm{45}^{} °\:\mathrm{with}\:\mathrm{the}\:\mathrm{line}\:\mathrm{AC}. \\ $$$$ \\ $$

Question Number 36034 Answers: 1 Comments: 1

Question Number 36031 Answers: 0 Comments: 0

Q. Evaluate: ∫_(∫xyzdxdydz) ^(∫zyxdzdydx) ∫_((d/dx)(x^(sin x) )) ^((d/dx)(x^(cos x) )) ∫_(lim_(x→0) ((−x^2 +2)/x)) ^(lim_(x→0) ((x^2 −2)/x)) ∫_0 ^∞ w^(1−x) x^(1−y) y^(1−z) z^(1−w) dwdxdydz

$$\mathrm{Q}.\:\mathrm{Evaluate}:\:\:\:\int_{\int\mathrm{xyzdxdydz}} ^{\int\mathrm{zyxdzdydx}} \int_{\frac{\mathrm{d}}{\mathrm{dx}}\left(\mathrm{x}^{\mathrm{sin}\:\mathrm{x}} \right)} ^{\frac{\mathrm{d}}{\mathrm{dx}}\left(\mathrm{x}^{\mathrm{cos}\:\mathrm{x}} \right)} \int_{\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\mathrm{x}^{\mathrm{2}} +\mathrm{2}}{\mathrm{x}}} ^{\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{2}}{\mathrm{x}}} \int_{\mathrm{0}} ^{\infty} \mathrm{w}^{\mathrm{1}−\mathrm{x}} \mathrm{x}^{\mathrm{1}−\mathrm{y}} \mathrm{y}^{\mathrm{1}−\mathrm{z}} \mathrm{z}^{\mathrm{1}−\mathrm{w}} \mathrm{dwdxdydz} \\ $$

Question Number 36030 Answers: 1 Comments: 1

Q. What will be the expression for area of sphere? If the area of cube is 4πr^2 . And all sides of cube touches the sphere.

$$\mathrm{Q}.\:\mathrm{What}\:\mathrm{will}\:\mathrm{be}\:\mathrm{the}\:\mathrm{expression}\:\mathrm{for}\:\mathrm{area}\:\mathrm{of}\:\mathrm{sphere}?\: \\ $$$$\:\:\:\:\:\:\:\:\mathrm{If}\:\mathrm{the}\:\mathrm{area}\:\mathrm{of}\:\mathrm{cube}\:\mathrm{is}\:\mathrm{4}\pi\mathrm{r}^{\mathrm{2}} .\:\mathrm{And}\:\mathrm{all}\:\mathrm{sides}\:\mathrm{of}\:\mathrm{cube}\:\mathrm{touches}\:\mathrm{the}\:\mathrm{sphere}. \\ $$

Question Number 36024 Answers: 1 Comments: 2

Question Number 36021 Answers: 0 Comments: 0

Prove that the hypotenuse never be even of a right angled triangle whose positive integer sides are relatively prime.

$$\mathrm{Prove}\:\mathrm{that}\:\mathrm{the}\:\mathrm{hypotenuse}\:\mathrm{never}\:\mathrm{be} \\ $$$$\mathrm{even}\:\mathrm{of}\:\mathrm{a}\:\mathrm{right}\:\mathrm{angled}\:\mathrm{triangle}\:\mathrm{whose} \\ $$$$\mathrm{positive}\:\mathrm{integer}\:\mathrm{sides}\:\mathrm{are}\:\mathrm{relatively}\:\mathrm{prime}. \\ $$

Question Number 36019 Answers: 3 Comments: 0

If a+b+c=0 show that ((a/(b−c))+(b/(c−a))+(c/(a−b)))(((b−c)/a)+((c−a)/b) +((a−b)/c))=9

$${If}\:{a}+{b}+{c}=\mathrm{0}\:{show}\:{that} \\ $$$$\left(\frac{{a}}{{b}−{c}}+\frac{{b}}{{c}−{a}}+\frac{{c}}{{a}−{b}}\right)\left(\frac{{b}−{c}}{{a}}+\frac{{c}−{a}}{{b}}\:+\frac{{a}−{b}}{{c}}\right)=\mathrm{9} \\ $$

Question Number 36018 Answers: 1 Comments: 0

Find the value of lim_(x→(π/2)) ((sinx−(sinx)^(sinx) )/(1−sinx+lnsinx))

$${Find}\:{the}\:{value}\:{of} \\ $$$$\underset{{x}\rightarrow\frac{\pi}{\mathrm{2}}} {{lim}}\:\frac{{sinx}−\left({sinx}\right)^{{sinx}} }{\mathrm{1}−{sinx}+{lnsinx}} \\ $$

Question Number 36011 Answers: 0 Comments: 2

simplify: ′interval number′ (1,6)∪(3,7)

$$\mathrm{simplify}:\:\:'{interval}\:{number}' \\ $$$$\left(\mathrm{1},\mathrm{6}\right)\cup\left(\mathrm{3},\mathrm{7}\right) \\ $$

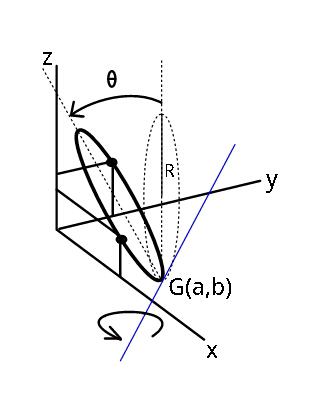
Question Number 36010 Answers: 0 Comments: 2

let f(x)= (x/(x^2 +x+1)) 1) calculate f^((n)) (0) 2) developp f at integr serie .

$${let}\:{f}\left({x}\right)=\:\:\frac{{x}}{{x}^{\mathrm{2}} \:+{x}+\mathrm{1}} \\ $$$$\left.\mathrm{1}\right)\:{calculate}\:{f}^{\left({n}\right)} \left(\mathrm{0}\right) \\ $$$$\left.\mathrm{2}\right)\:{developp}\:{f}\:\:{at}\:{integr}\:{serie}\:. \\ $$

Question Number 36009 Answers: 0 Comments: 1

calculate ∫_(−∞) ^(+∞) ((xdx)/((2x+1+i)^3 )) with i^2 =−1 .

$${calculate}\:\int_{−\infty} ^{+\infty} \:\:\:\:\:\frac{{xdx}}{\left(\mathrm{2}{x}+\mathrm{1}+{i}\right)^{\mathrm{3}} }\:\:{with}\:{i}^{\mathrm{2}} \:=−\mathrm{1}\:. \\ $$

Question Number 35990 Answers: 0 Comments: 2

calculate ∫_2 ^5 ((xdx)/(2x+1 +(√(x−1))))

$${calculate}\:\int_{\mathrm{2}} ^{\mathrm{5}} \:\:\:\:\frac{{xdx}}{\mathrm{2}{x}+\mathrm{1}\:+\sqrt{{x}−\mathrm{1}}} \\ $$

Question Number 35988 Answers: 1 Comments: 2

let f(x) = ((x+2)/(x^3 −4x +3)) 1) calculate f^((n)) (x) 2) developp f at integr serie.

$${let}\:{f}\left({x}\right)\:=\:\frac{{x}+\mathrm{2}}{{x}^{\mathrm{3}} −\mathrm{4}{x}\:+\mathrm{3}} \\ $$$$\left.\mathrm{1}\right)\:{calculate}\:{f}^{\left({n}\right)} \left({x}\right) \\ $$$$\left.\mathrm{2}\right)\:{developp}\:{f}\:{at}\:{integr}\:{serie}. \\ $$

Question Number 35987 Answers: 0 Comments: 4

let f(x) = (1/(1+x^3 )) 1) calculate f^((n)) (x) 2) developp f at integr serie.

$${let}\:{f}\left({x}\right)\:=\:\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{3}} } \\ $$$$\left.\mathrm{1}\right)\:{calculate}\:{f}^{\left({n}\right)} \left({x}\right) \\ $$$$\left.\mathrm{2}\right)\:{developp}\:{f}\:{at}\:{integr}\:{serie}. \\ $$

Question Number 35986 Answers: 0 Comments: 5

let f(x)= (√(1 +n x^2 )) −nx +3 with n integr 1) calculate lim_(x→+∞) and lim_(x→−∞) f(x) 2) calculate f^′ (x) 3) give the equation of assymptote of f at point A(1,f(1)) . 4)calculate lim_(x→+∞) ((f(x))/x) and lim_(x→−∞) ((f(x))/x) .

$${let}\:{f}\left({x}\right)=\:\sqrt{\mathrm{1}\:+{n}\:{x}^{\mathrm{2}} }\:\:\:−{nx}\:+\mathrm{3}\:\:{with}\:{n}\:{integr} \\ $$$$\left.\mathrm{1}\right)\:{calculate}\:{lim}_{{x}\rightarrow+\infty} \:{and}\:{lim}_{{x}\rightarrow−\infty} {f}\left({x}\right) \\ $$$$\left.\mathrm{2}\right)\:{calculate}\:{f}^{'} \left({x}\right) \\ $$$$\left.\mathrm{3}\right)\:{give}\:{the}\:{equation}\:{of}\:{assymptote}\:{of}\:{f}\:{at} \\ $$$${point}\:\:{A}\left(\mathrm{1},{f}\left(\mathrm{1}\right)\right)\:. \\ $$$$\left.\mathrm{4}\right){calculate}\:{lim}_{{x}\rightarrow+\infty} \:\frac{{f}\left({x}\right)}{{x}}\:{and}\:{lim}_{{x}\rightarrow−\infty} \:\:\frac{{f}\left({x}\right)}{{x}}\:. \\ $$

Question Number 35983 Answers: 0 Comments: 1

calculate ∫_0 ^∞ ((2(√t) +1)/(t^5 +3))dt .

$${calculate}\:\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\frac{\mathrm{2}\sqrt{{t}}\:+\mathrm{1}}{{t}^{\mathrm{5}} \:\:\:+\mathrm{3}}{dt}\:\:. \\ $$

Question Number 35982 Answers: 0 Comments: 0

let f(t) =∫_0 ^∞ e^(−arctsn( 1+tx^2 )) dx with t from R 1) calculate f^′ (t) 2) find a simple form of f(t) .

$${let}\:{f}\left({t}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\:\:{e}^{−{arctsn}\left(\:\mathrm{1}+{tx}^{\mathrm{2}} \right)} {dx}\:\:{with}\:{t}\:{from}\:{R} \\ $$$$\left.\mathrm{1}\right)\:{calculate}\:{f}^{'} \left({t}\right) \\ $$$$\left.\mathrm{2}\right)\:{find}\:{a}\:{simple}\:{form}\:{of}\:{f}\left({t}\right)\:. \\ $$

Question Number 36003 Answers: 2 Comments: 0

x [(2),(1) ]+y [(3),(5) ]+ [((−8)),((−11)) ]=0 find x and y

$${x}\begin{bmatrix}{\mathrm{2}}\\{\mathrm{1}}\end{bmatrix}+{y}\begin{bmatrix}{\mathrm{3}}\\{\mathrm{5}}\end{bmatrix}+\begin{bmatrix}{−\mathrm{8}}\\{−\mathrm{11}}\end{bmatrix}=\mathrm{0} \\ $$$${find}\:{x}\:{and}\:{y} \\ $$

Question Number 35968 Answers: 2 Comments: 1

Question Number 35960 Answers: 0 Comments: 3

Solve using Residue Theorem I = ∫_(−∞) ^(+∞) (x^2 /(x^4 + 16)) dx

$$\mathrm{Solve}\:\mathrm{using}\:\mathrm{Residue}\:\mathrm{Theorem} \\ $$$$\mathrm{I}\:=\:\int_{−\infty} ^{+\infty} \:\frac{{x}^{\mathrm{2}} }{{x}^{\mathrm{4}} \:+\:\mathrm{16}}\:{dx} \\ $$

Pg 1626 Pg 1627 Pg 1628 Pg 1629 Pg 1630 Pg 1631 Pg 1632 Pg 1633 Pg 1634 Pg 1635

Contact: info@tinkutara.com