
AllQuestion and Answers: Page 1615
Question Number 44467 Answers: 1 Comments: 0
Question Number 44466 Answers: 0 Comments: 4
Question Number 44454 Answers: 0 Comments: 4

Question Number 44444 Answers: 1 Comments: 0
Question Number 44441 Answers: 1 Comments: 0

Question Number 44436 Answers: 1 Comments: 1
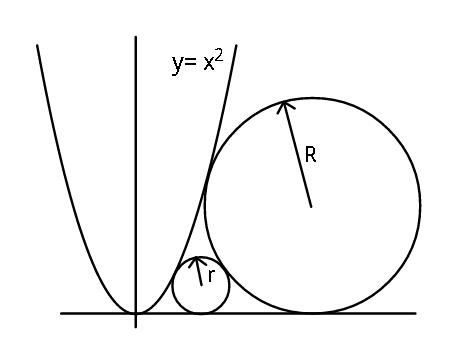
Question Number 44430 Answers: 0 Comments: 0

Question Number 44424 Answers: 1 Comments: 0
Question Number 44423 Answers: 1 Comments: 0
Question Number 44422 Answers: 0 Comments: 3
Question Number 44411 Answers: 0 Comments: 0
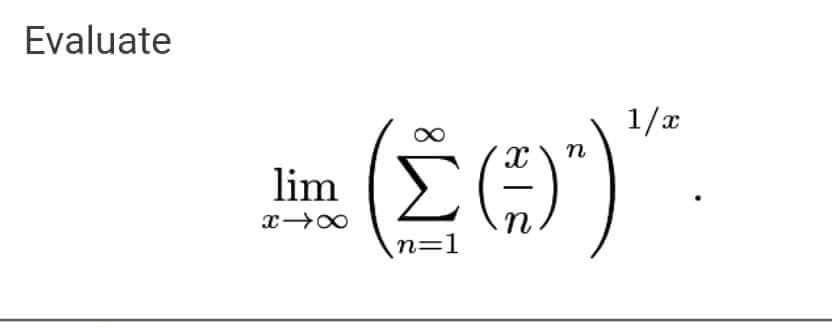
Question Number 44397 Answers: 2 Comments: 4
Question Number 44395 Answers: 1 Comments: 3

Question Number 44389 Answers: 0 Comments: 0
Question Number 44387 Answers: 0 Comments: 0

Question Number 44384 Answers: 2 Comments: 6
Question Number 44374 Answers: 1 Comments: 0

Question Number 44373 Answers: 1 Comments: 0

Question Number 44369 Answers: 1 Comments: 1
Question Number 44365 Answers: 2 Comments: 1

Question Number 44356 Answers: 0 Comments: 0

Question Number 44355 Answers: 0 Comments: 0

Question Number 44351 Answers: 1 Comments: 1
Question Number 44350 Answers: 0 Comments: 3
Question Number 44346 Answers: 0 Comments: 0
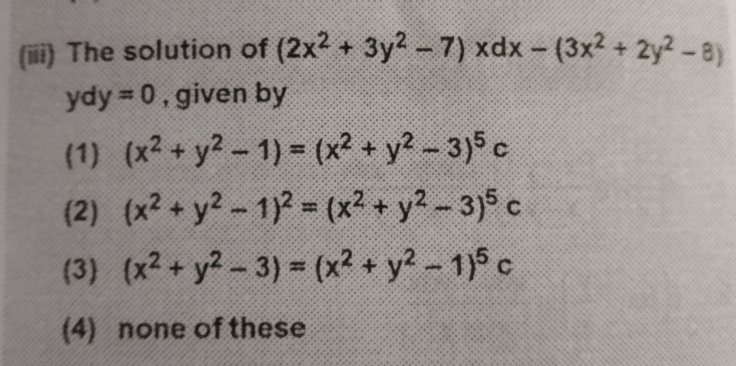
Question Number 44336 Answers: 0 Comments: 0

Pg 1610 Pg 1611 Pg 1612 Pg 1613 Pg 1614 Pg 1615 Pg 1616 Pg 1617 Pg 1618 Pg 1619
