
AllQuestion and Answers: Page 1612
Question Number 48874 Answers: 2 Comments: 1

Question Number 48872 Answers: 0 Comments: 1

Question Number 48871 Answers: 3 Comments: 1

Question Number 48869 Answers: 1 Comments: 3

Question Number 48852 Answers: 1 Comments: 0
Question Number 48851 Answers: 1 Comments: 9
Question Number 48846 Answers: 0 Comments: 1
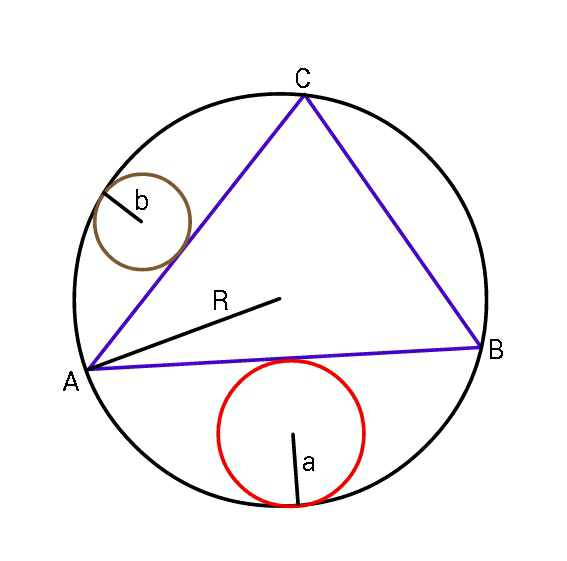
Question Number 48845 Answers: 1 Comments: 1

Question Number 48843 Answers: 0 Comments: 0

Question Number 48841 Answers: 0 Comments: 0
Question Number 48849 Answers: 1 Comments: 0
Question Number 48837 Answers: 1 Comments: 0
Question Number 48833 Answers: 1 Comments: 4

Question Number 48830 Answers: 1 Comments: 0
Question Number 48829 Answers: 0 Comments: 3
Question Number 48826 Answers: 1 Comments: 0
Question Number 48823 Answers: 1 Comments: 3

Question Number 48815 Answers: 0 Comments: 7
Question Number 48795 Answers: 1 Comments: 1
Question Number 48777 Answers: 0 Comments: 13

Question Number 48769 Answers: 1 Comments: 0

Question Number 48763 Answers: 2 Comments: 1

Question Number 48757 Answers: 2 Comments: 2
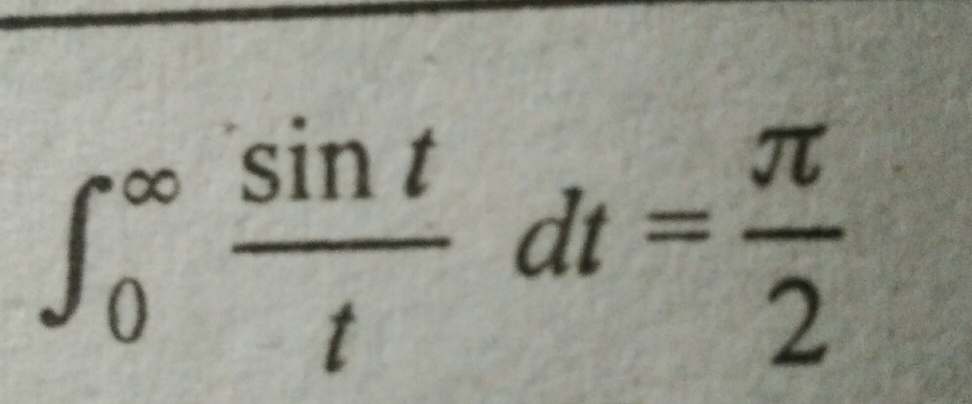
Question Number 48750 Answers: 1 Comments: 0
Question Number 48748 Answers: 0 Comments: 0

Question Number 48745 Answers: 1 Comments: 0

Pg 1607 Pg 1608 Pg 1609 Pg 1610 Pg 1611 Pg 1612 Pg 1613 Pg 1614 Pg 1615 Pg 1616
