
AllQuestion and Answers: Page 1611
Question Number 48498 Answers: 2 Comments: 4
Question Number 48497 Answers: 0 Comments: 5
Question Number 48496 Answers: 0 Comments: 0
Question Number 48493 Answers: 2 Comments: 1
Question Number 48495 Answers: 1 Comments: 1
Question Number 48494 Answers: 1 Comments: 0
Question Number 48491 Answers: 0 Comments: 0
Question Number 48489 Answers: 0 Comments: 0

Question Number 48484 Answers: 1 Comments: 0
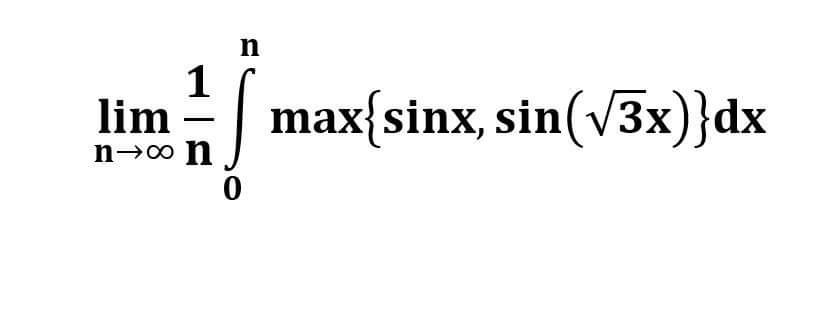
Question Number 48482 Answers: 0 Comments: 0
Question Number 48474 Answers: 2 Comments: 0
Question Number 48466 Answers: 1 Comments: 0
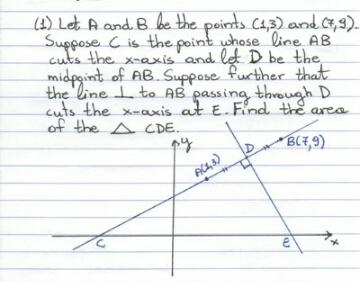
Question Number 48460 Answers: 1 Comments: 2
Question Number 48458 Answers: 1 Comments: 1

Question Number 48447 Answers: 0 Comments: 4
Question Number 48443 Answers: 1 Comments: 3
Question Number 48435 Answers: 1 Comments: 0
Question Number 48434 Answers: 2 Comments: 0

Question Number 48433 Answers: 1 Comments: 0
Question Number 48426 Answers: 0 Comments: 4
Question Number 48405 Answers: 0 Comments: 7
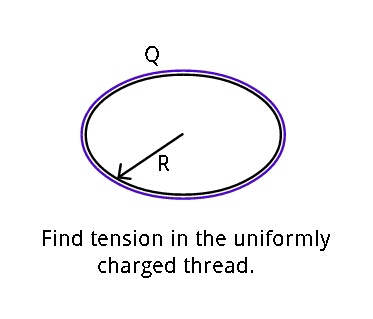
Question Number 48396 Answers: 2 Comments: 2

Question Number 48388 Answers: 2 Comments: 1
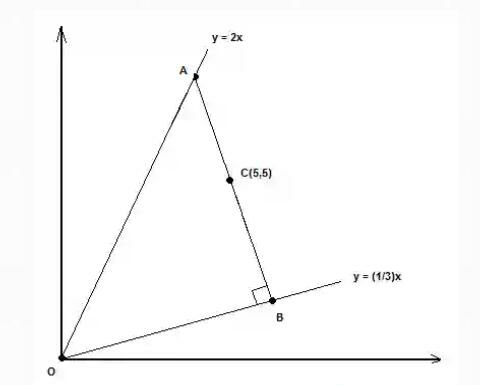
Question Number 48384 Answers: 1 Comments: 1
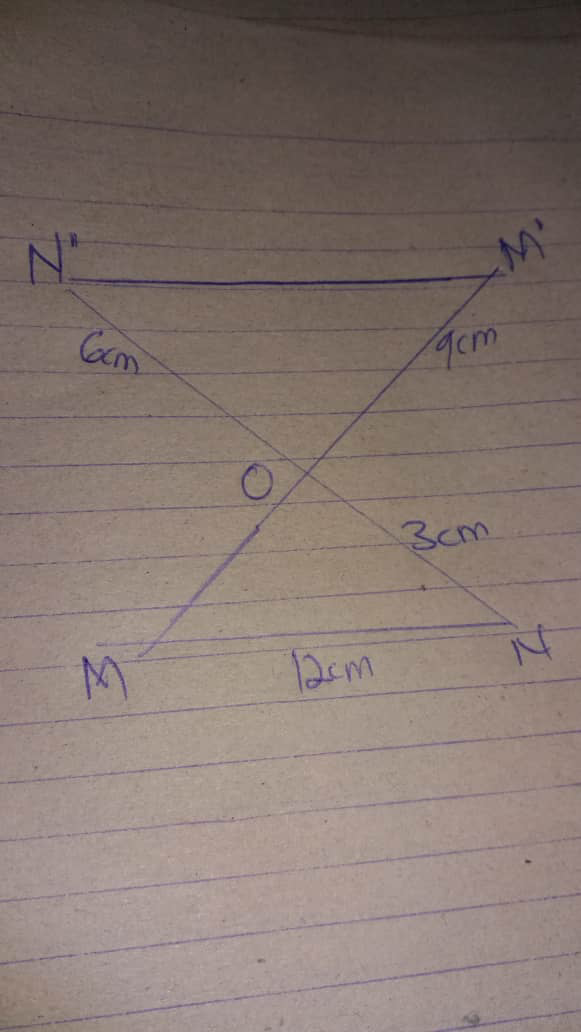
Question Number 48374 Answers: 0 Comments: 0
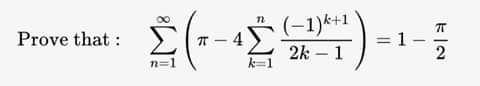
Question Number 48368 Answers: 1 Comments: 0
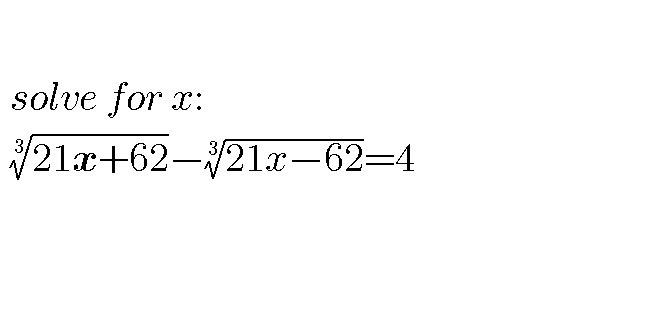
Pg 1606 Pg 1607 Pg 1608 Pg 1609 Pg 1610 Pg 1611 Pg 1612 Pg 1613 Pg 1614 Pg 1615
