
AllQuestion and Answers: Page 1609
Question Number 48769 Answers: 1 Comments: 0

Question Number 48763 Answers: 2 Comments: 1

Question Number 48757 Answers: 2 Comments: 2
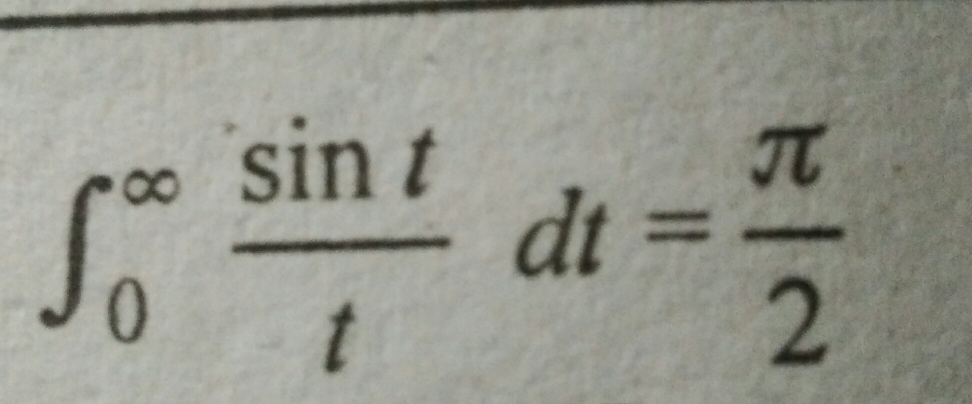
Question Number 48750 Answers: 1 Comments: 0
Question Number 48748 Answers: 0 Comments: 0

Question Number 48745 Answers: 1 Comments: 0

Question Number 48744 Answers: 2 Comments: 0

Question Number 48742 Answers: 1 Comments: 0

Question Number 48741 Answers: 1 Comments: 0

Question Number 48740 Answers: 2 Comments: 1

Question Number 48739 Answers: 1 Comments: 0
Question Number 48736 Answers: 1 Comments: 0
Question Number 48735 Answers: 1 Comments: 0
Question Number 48729 Answers: 1 Comments: 0

Question Number 48725 Answers: 1 Comments: 3
Question Number 48724 Answers: 1 Comments: 1
Question Number 48720 Answers: 0 Comments: 2
Question Number 48719 Answers: 1 Comments: 1
Question Number 48718 Answers: 1 Comments: 2
Question Number 48717 Answers: 0 Comments: 1
Question Number 48715 Answers: 0 Comments: 4
Question Number 48711 Answers: 1 Comments: 1

Question Number 48703 Answers: 1 Comments: 0

Question Number 48687 Answers: 0 Comments: 0
Question Number 48705 Answers: 3 Comments: 2
Question Number 48678 Answers: 0 Comments: 0

Pg 1604 Pg 1605 Pg 1606 Pg 1607 Pg 1608 Pg 1609 Pg 1610 Pg 1611 Pg 1612 Pg 1613
