
AllQuestion and Answers: Page 1608
Question Number 49294 Answers: 1 Comments: 0
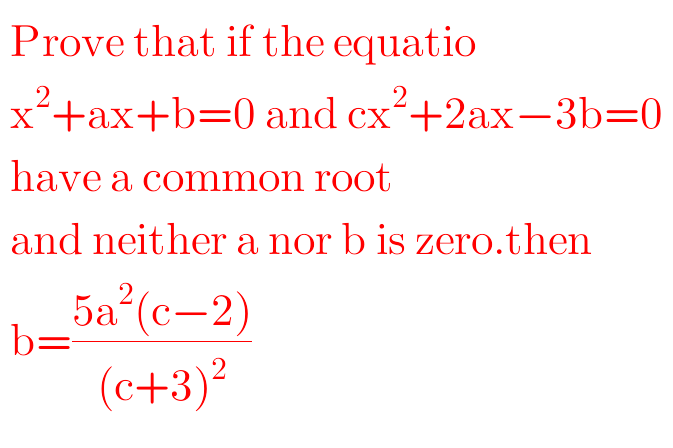
Question Number 49283 Answers: 1 Comments: 0
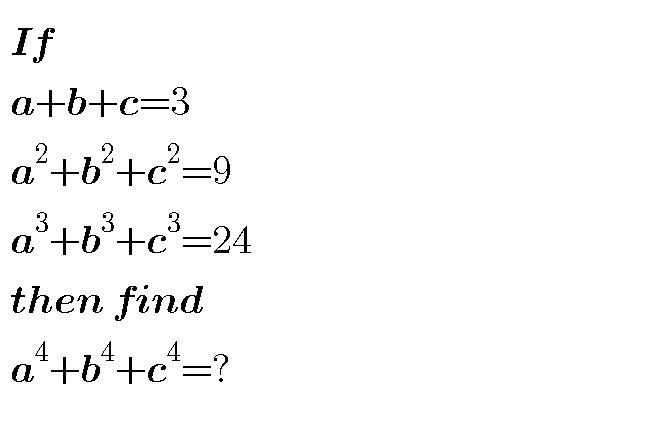
Question Number 49280 Answers: 1 Comments: 3

Question Number 49272 Answers: 2 Comments: 0
Question Number 49279 Answers: 2 Comments: 1
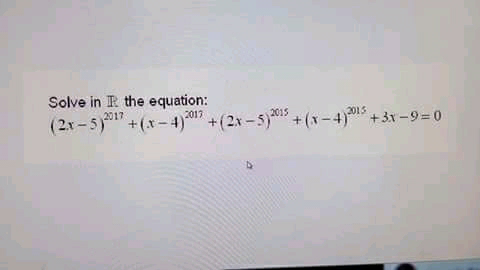
Question Number 49256 Answers: 2 Comments: 0

Question Number 49253 Answers: 2 Comments: 0

Question Number 49252 Answers: 1 Comments: 0
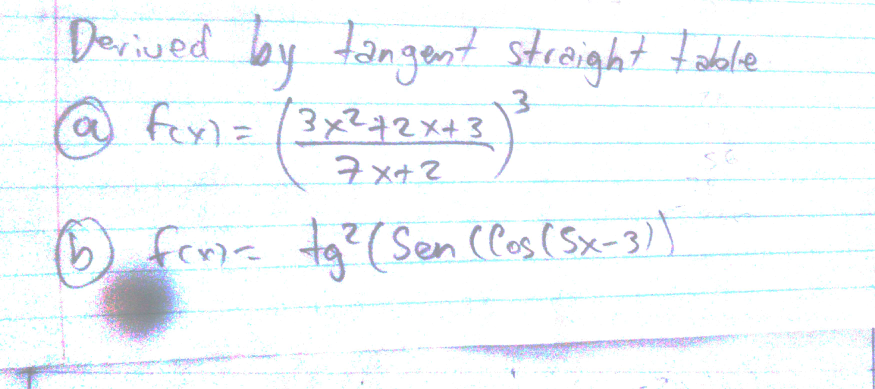
Question Number 49251 Answers: 5 Comments: 1

Question Number 49250 Answers: 1 Comments: 0
Question Number 49248 Answers: 1 Comments: 0
Question Number 49244 Answers: 1 Comments: 0
Question Number 49246 Answers: 0 Comments: 0
Question Number 49245 Answers: 0 Comments: 0
Question Number 49242 Answers: 0 Comments: 0
Question Number 49241 Answers: 0 Comments: 0
Question Number 49249 Answers: 0 Comments: 0
Question Number 49238 Answers: 0 Comments: 3
Question Number 49237 Answers: 0 Comments: 0
Question Number 49236 Answers: 0 Comments: 2
Question Number 49235 Answers: 0 Comments: 0
Question Number 49232 Answers: 0 Comments: 2
Question Number 49230 Answers: 0 Comments: 0

Question Number 49229 Answers: 0 Comments: 4
$$\boldsymbol{{x}}^{\mathrm{2}} −\boldsymbol{{y}}^{\mathrm{2}} \\ $$
Question Number 49225 Answers: 1 Comments: 0
$$\int\frac{\mathrm{1}}{{z}\left({z}^{\mathrm{17}} +\mathrm{1}\right)}=??\:{find}\:{please} \\ $$
Question Number 49222 Answers: 0 Comments: 0

Pg 1603 Pg 1604 Pg 1605 Pg 1606 Pg 1607 Pg 1608 Pg 1609 Pg 1610 Pg 1611 Pg 1612
