
AllQuestion and Answers: Page 1606
Question Number 49555 Answers: 0 Comments: 0
$$\mathrm{Find}\:\mathrm{4}\:\: \\ $$$$\mathrm{plz}\:\mathrm{help}\:\mathrm{me}\:\mathrm{sir} \\ $$
Question Number 49554 Answers: 0 Comments: 0
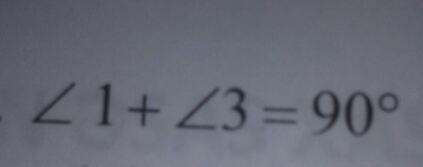
Question Number 49553 Answers: 0 Comments: 1

Question Number 49536 Answers: 3 Comments: 2
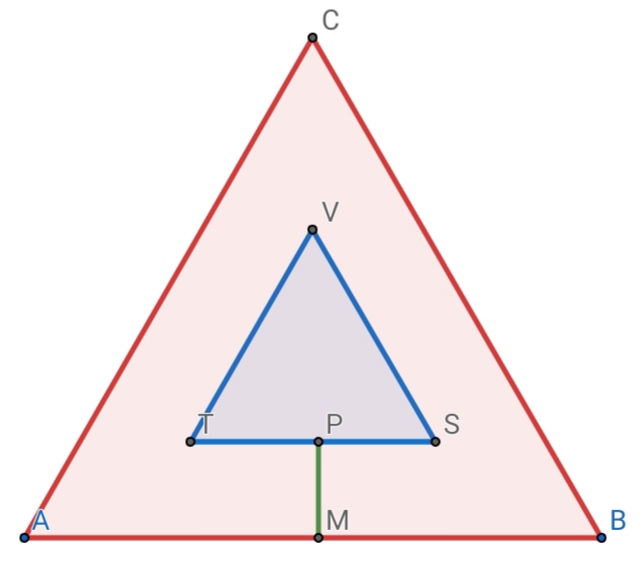
Question Number 49534 Answers: 1 Comments: 3
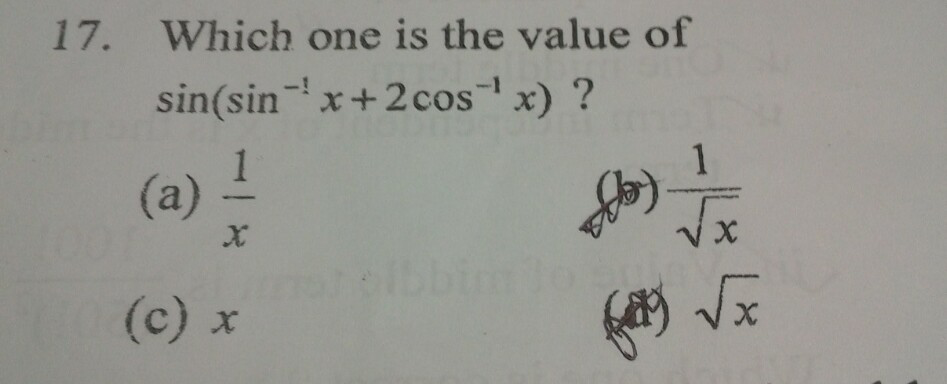
Question Number 49530 Answers: 3 Comments: 3

Question Number 49526 Answers: 1 Comments: 1

Question Number 49583 Answers: 0 Comments: 4
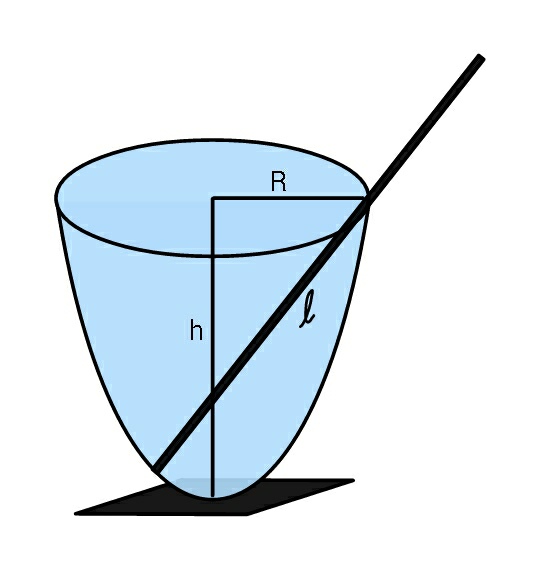
Question Number 49491 Answers: 1 Comments: 0
Question Number 49487 Answers: 0 Comments: 2
Question Number 49482 Answers: 1 Comments: 14
Question Number 49468 Answers: 1 Comments: 0
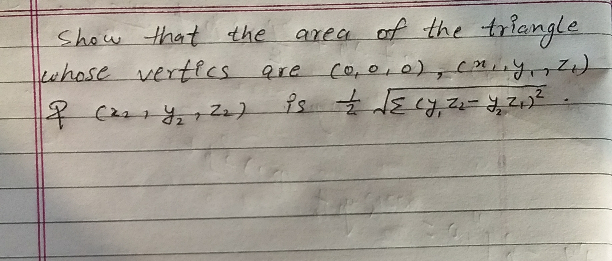
Question Number 49466 Answers: 0 Comments: 0
Question Number 49464 Answers: 2 Comments: 2
Question Number 49463 Answers: 1 Comments: 0
Question Number 49462 Answers: 2 Comments: 0
Question Number 49461 Answers: 2 Comments: 0
Question Number 49460 Answers: 0 Comments: 2
Question Number 49459 Answers: 2 Comments: 0
Question Number 49457 Answers: 0 Comments: 0
$${evaluate}\:\int{x}^{\mathrm{3}\:} {J}_{\mathrm{3}} \left({x}\right){dx} \\ $$
Question Number 49433 Answers: 3 Comments: 6

Question Number 49430 Answers: 0 Comments: 1

Question Number 49427 Answers: 0 Comments: 1
Question Number 49408 Answers: 1 Comments: 3
Question Number 49396 Answers: 0 Comments: 0
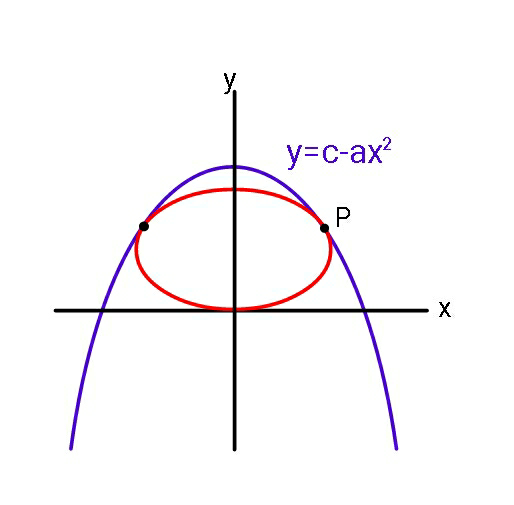
Question Number 49394 Answers: 1 Comments: 1
Pg 1601 Pg 1602 Pg 1603 Pg 1604 Pg 1605 Pg 1606 Pg 1607 Pg 1608 Pg 1609 Pg 1610
