
AllQuestion and Answers: Page 1602
Question Number 49987 Answers: 1 Comments: 4
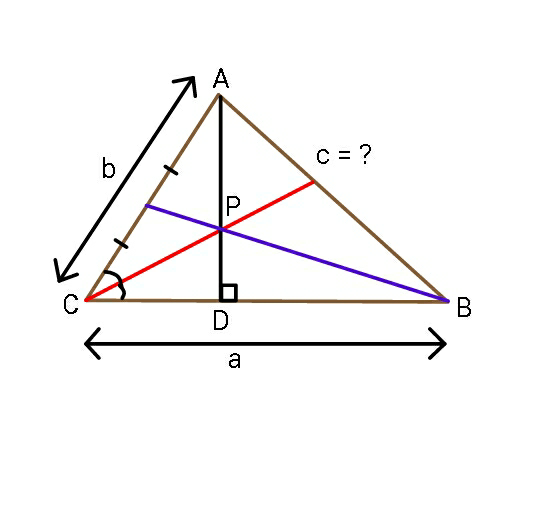
Question Number 49984 Answers: 1 Comments: 1

Question Number 49983 Answers: 1 Comments: 0
Question Number 49982 Answers: 1 Comments: 0
Question Number 49976 Answers: 0 Comments: 3
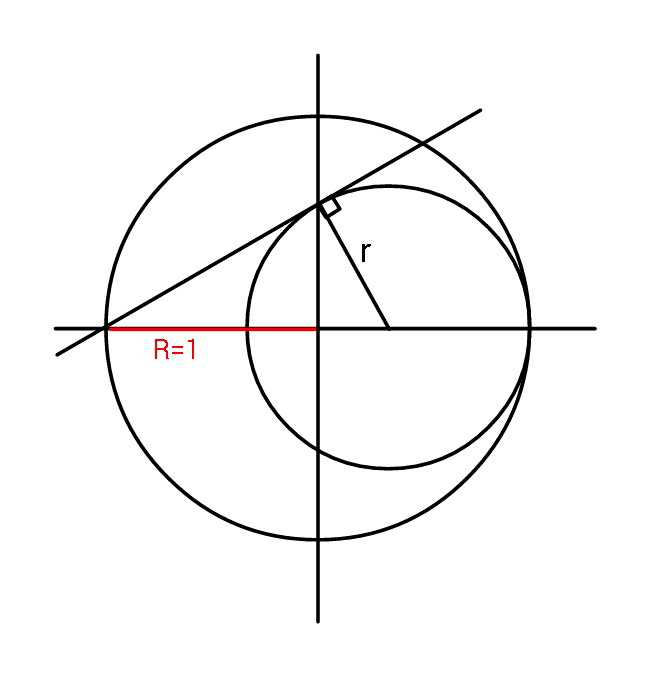
Question Number 49970 Answers: 2 Comments: 1
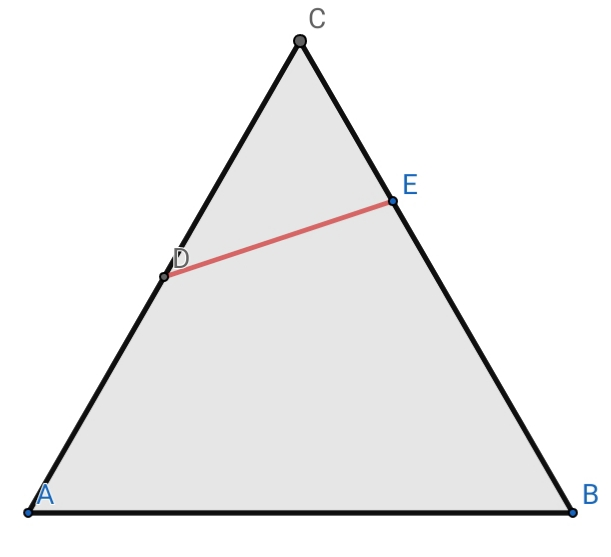
Question Number 49968 Answers: 0 Comments: 1
Question Number 49967 Answers: 0 Comments: 1
Question Number 49966 Answers: 1 Comments: 1
Question Number 49964 Answers: 1 Comments: 2
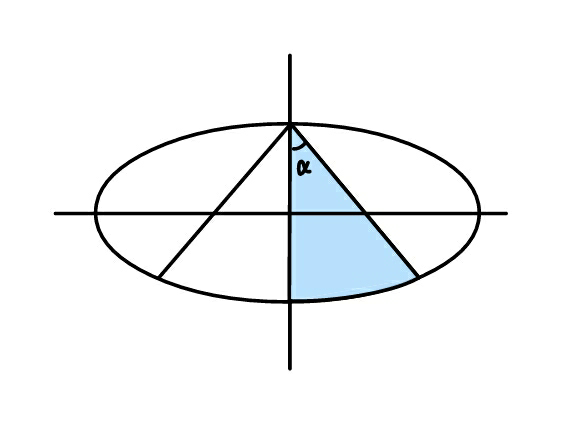
Question Number 49963 Answers: 0 Comments: 0
Question Number 49961 Answers: 0 Comments: 1
Question Number 49956 Answers: 1 Comments: 1
Question Number 49953 Answers: 0 Comments: 3
Question Number 49952 Answers: 0 Comments: 2
Question Number 49950 Answers: 1 Comments: 1

Question Number 49954 Answers: 1 Comments: 1
Question Number 49942 Answers: 0 Comments: 1
Question Number 49941 Answers: 0 Comments: 3
Question Number 49939 Answers: 0 Comments: 4
Question Number 49938 Answers: 0 Comments: 1
Question Number 49937 Answers: 1 Comments: 2
Question Number 49935 Answers: 2 Comments: 1
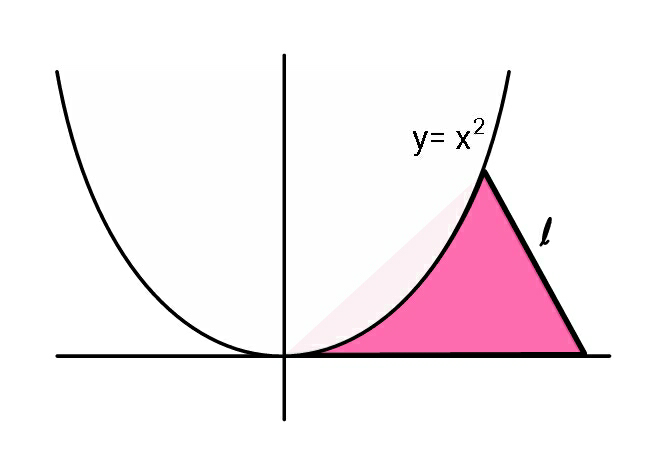
Question Number 49930 Answers: 1 Comments: 0
Question Number 49927 Answers: 0 Comments: 2
Question Number 49922 Answers: 1 Comments: 0
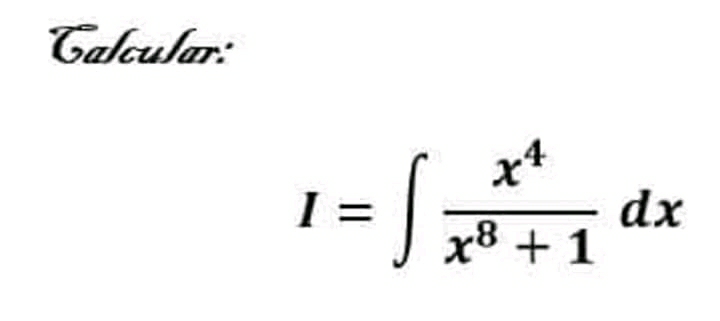
Pg 1597 Pg 1598 Pg 1599 Pg 1600 Pg 1601 Pg 1602 Pg 1603 Pg 1604 Pg 1605 Pg 1606
