
AllQuestion and Answers: Page 1601
Question Number 49696 Answers: 1 Comments: 1

Question Number 49680 Answers: 1 Comments: 0

Question Number 49678 Answers: 1 Comments: 1
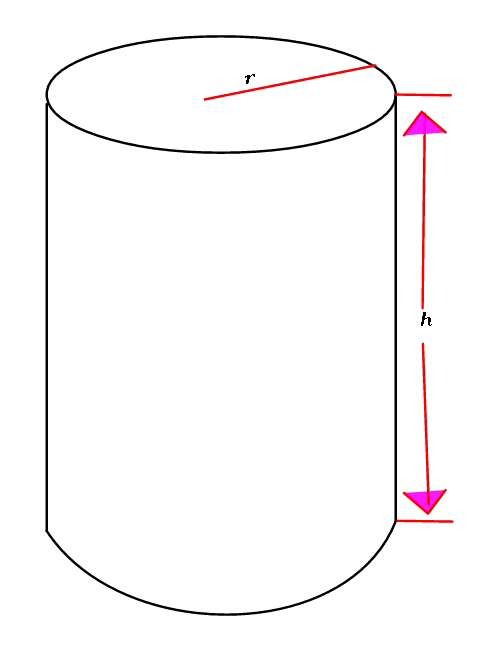
Question Number 50924 Answers: 1 Comments: 0
Question Number 49692 Answers: 1 Comments: 0
Question Number 49691 Answers: 1 Comments: 0
Question Number 49748 Answers: 1 Comments: 0
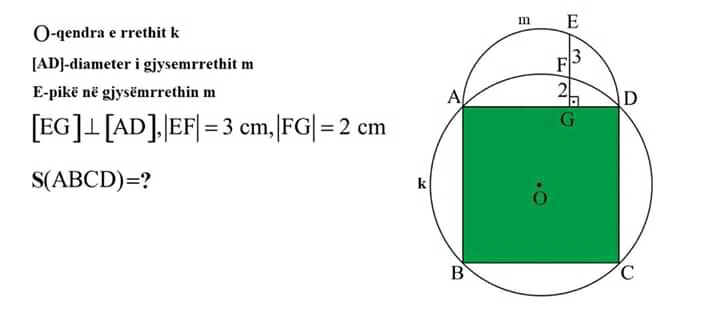
Question Number 49661 Answers: 1 Comments: 2
Question Number 49660 Answers: 2 Comments: 1
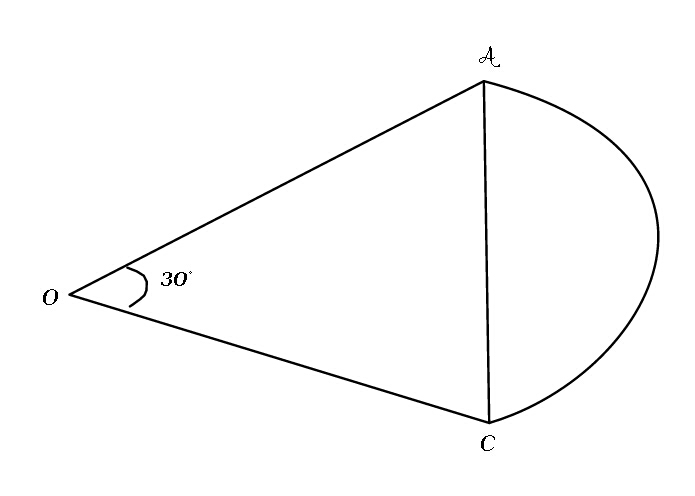
Question Number 49647 Answers: 1 Comments: 3
Question Number 49646 Answers: 0 Comments: 0
Question Number 49645 Answers: 1 Comments: 0
Question Number 70360 Answers: 1 Comments: 0
Question Number 49642 Answers: 1 Comments: 0
Question Number 49640 Answers: 1 Comments: 2
Question Number 49639 Answers: 1 Comments: 1
Question Number 49638 Answers: 1 Comments: 0
Question Number 49637 Answers: 1 Comments: 0

Question Number 49636 Answers: 1 Comments: 2
Question Number 49635 Answers: 1 Comments: 1
Question Number 49621 Answers: 0 Comments: 0

Question Number 49605 Answers: 1 Comments: 3

Question Number 49604 Answers: 2 Comments: 0
Question Number 49602 Answers: 0 Comments: 0
Question Number 71170 Answers: 1 Comments: 1

Question Number 49594 Answers: 0 Comments: 1
$$\:\:\:\:{How}\:{can}\:{we}\:{insert}\:{images}\:{in}\:{the}\:{editor}? \\ $$
Pg 1596 Pg 1597 Pg 1598 Pg 1599 Pg 1600 Pg 1601 Pg 1602 Pg 1603 Pg 1604 Pg 1605
