
AllQuestion and Answers: Page 1600
Question Number 50226 Answers: 0 Comments: 1
Question Number 50220 Answers: 0 Comments: 4
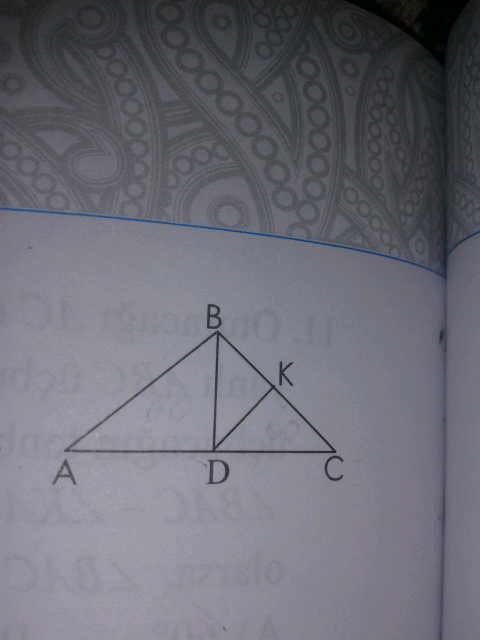
Question Number 50219 Answers: 7 Comments: 0

Question Number 50423 Answers: 1 Comments: 1
Question Number 50209 Answers: 1 Comments: 0
Question Number 50201 Answers: 0 Comments: 2
$$\mathrm{a}=\mathrm{665},\mathrm{21}\:\:\:\:\:\:\:\mathrm{b}=\mathrm{47},\mathrm{14} \\ $$
Question Number 50198 Answers: 0 Comments: 1
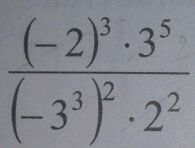
Question Number 50197 Answers: 0 Comments: 0
$$\mathrm{plz}\:\mathrm{plz}\:\mathrm{help}\:\mathrm{me}\:\mathrm{sir} \\ $$
Question Number 50196 Answers: 0 Comments: 0
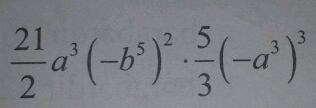
Question Number 50195 Answers: 0 Comments: 0

Question Number 50194 Answers: 0 Comments: 2

Question Number 50349 Answers: 0 Comments: 0

Question Number 50200 Answers: 0 Comments: 2
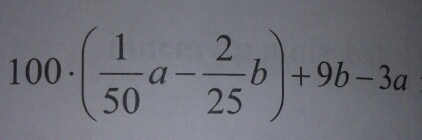
Question Number 50239 Answers: 1 Comments: 1

Question Number 50186 Answers: 1 Comments: 0
Question Number 50175 Answers: 1 Comments: 0

Question Number 50171 Answers: 0 Comments: 3
Question Number 50163 Answers: 2 Comments: 0

Question Number 50161 Answers: 1 Comments: 0
Question Number 50158 Answers: 7 Comments: 1

Question Number 50156 Answers: 0 Comments: 1

Question Number 50155 Answers: 0 Comments: 1
$$\mathrm{plz}\:\mathrm{help}\:\mathrm{me}\:\mathrm{sir} \\ $$
Question Number 50140 Answers: 5 Comments: 0
Question Number 50138 Answers: 0 Comments: 1
Question Number 50135 Answers: 2 Comments: 2

Question Number 50132 Answers: 0 Comments: 1
Pg 1595 Pg 1596 Pg 1597 Pg 1598 Pg 1599 Pg 1600 Pg 1601 Pg 1602 Pg 1603 Pg 1604
