
AllQuestion and Answers: Page 1597
Question Number 50163 Answers: 2 Comments: 0

Question Number 50161 Answers: 1 Comments: 0
Question Number 50158 Answers: 7 Comments: 1

Question Number 50156 Answers: 0 Comments: 1

Question Number 50155 Answers: 0 Comments: 1
$$\mathrm{plz}\:\mathrm{help}\:\mathrm{me}\:\mathrm{sir} \\ $$
Question Number 50140 Answers: 5 Comments: 0
Question Number 50138 Answers: 0 Comments: 1
Question Number 50135 Answers: 2 Comments: 2

Question Number 50132 Answers: 0 Comments: 1
Question Number 50126 Answers: 0 Comments: 0

Question Number 50125 Answers: 0 Comments: 2
$$\mathrm{help}\:\mathrm{me}\:\mathrm{plz}\:\mathrm{sir} \\ $$
Question Number 50101 Answers: 2 Comments: 4

Question Number 50093 Answers: 2 Comments: 1

Question Number 50089 Answers: 1 Comments: 2
Question Number 50085 Answers: 0 Comments: 0
Question Number 50084 Answers: 0 Comments: 0
$$\mathrm{could}\:\mathrm{you}\:\mathrm{help}\:\mathrm{me}\:\mathrm{sir}? \\ $$
Question Number 50083 Answers: 0 Comments: 0
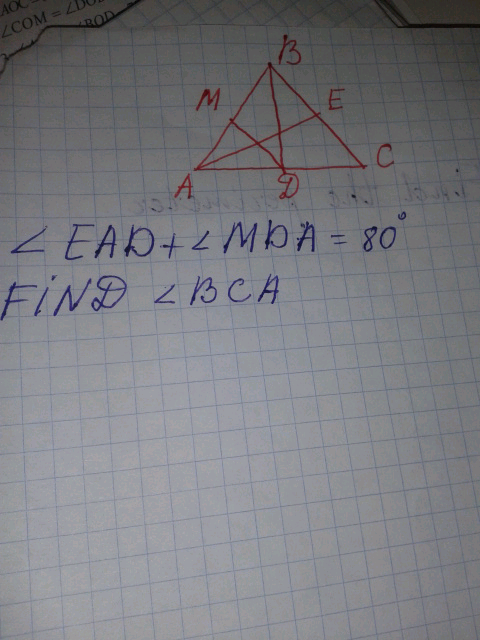
Question Number 50080 Answers: 1 Comments: 0
Question Number 50065 Answers: 3 Comments: 0

Question Number 50064 Answers: 3 Comments: 0
Question Number 50052 Answers: 5 Comments: 1
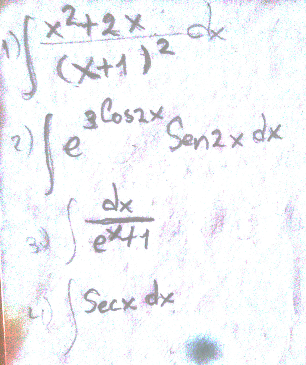
Question Number 50047 Answers: 1 Comments: 0

Question Number 50048 Answers: 3 Comments: 4
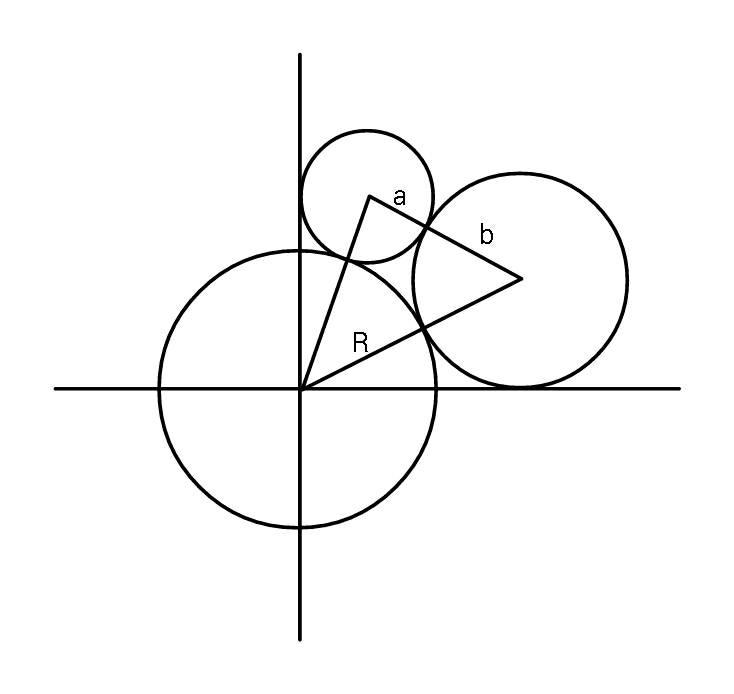
Question Number 50017 Answers: 0 Comments: 4
Question Number 50016 Answers: 2 Comments: 0
Question Number 50012 Answers: 0 Comments: 0
$$\mathrm{help}\:\mathrm{me}\:\mathrm{sir}\:\mathrm{plz} \\ $$$$ \\ $$$$ \\ $$
Pg 1592 Pg 1593 Pg 1594 Pg 1595 Pg 1596 Pg 1597 Pg 1598 Pg 1599 Pg 1600 Pg 1601
