
AllQuestion and Answers: Page 1596
Question Number 50580 Answers: 2 Comments: 0
Question Number 50577 Answers: 1 Comments: 1
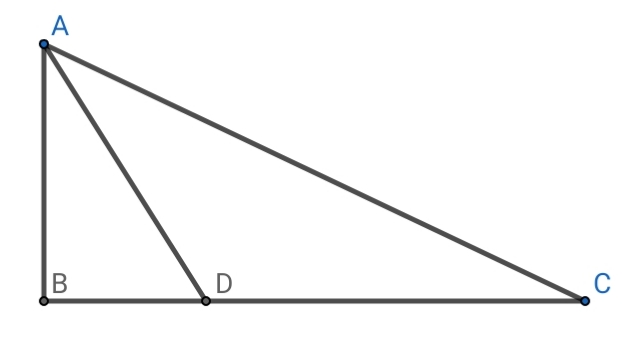
Question Number 50576 Answers: 0 Comments: 1
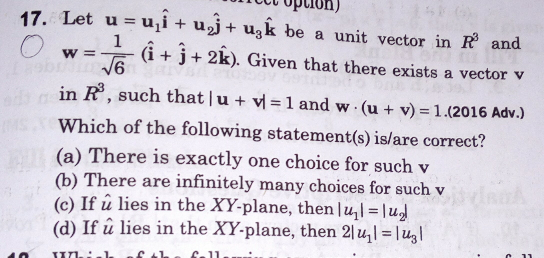
Question Number 50573 Answers: 0 Comments: 0

Question Number 50568 Answers: 1 Comments: 1
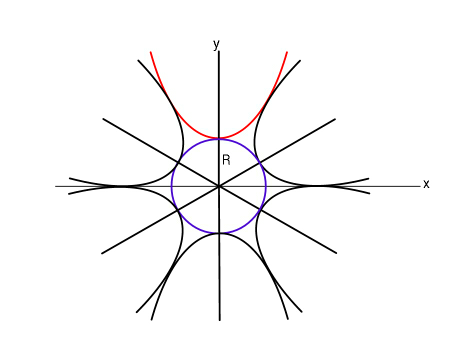
Question Number 50657 Answers: 0 Comments: 0

Question Number 50561 Answers: 3 Comments: 1
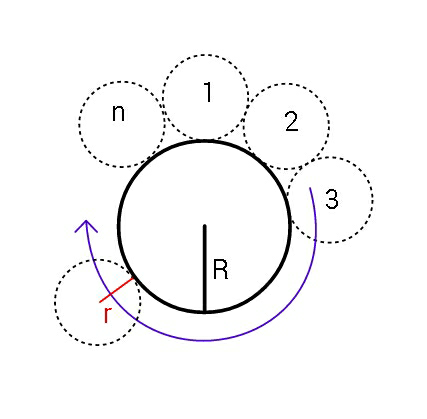
Question Number 50560 Answers: 1 Comments: 0
Question Number 50558 Answers: 0 Comments: 0
Question Number 50553 Answers: 0 Comments: 2
Question Number 50551 Answers: 1 Comments: 0
Question Number 50549 Answers: 1 Comments: 0
Question Number 50547 Answers: 2 Comments: 0

Question Number 50519 Answers: 3 Comments: 0

Question Number 50511 Answers: 1 Comments: 0
Question Number 50466 Answers: 0 Comments: 4
Question Number 50460 Answers: 2 Comments: 2
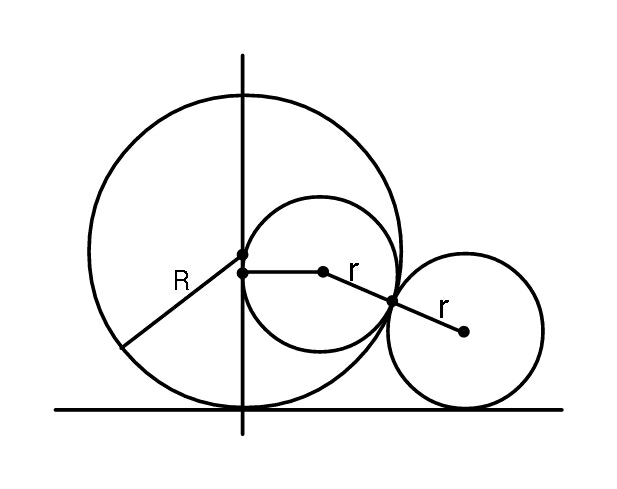
Question Number 50453 Answers: 0 Comments: 3

Question Number 50451 Answers: 2 Comments: 0
Question Number 50450 Answers: 0 Comments: 0
Question Number 50446 Answers: 0 Comments: 2
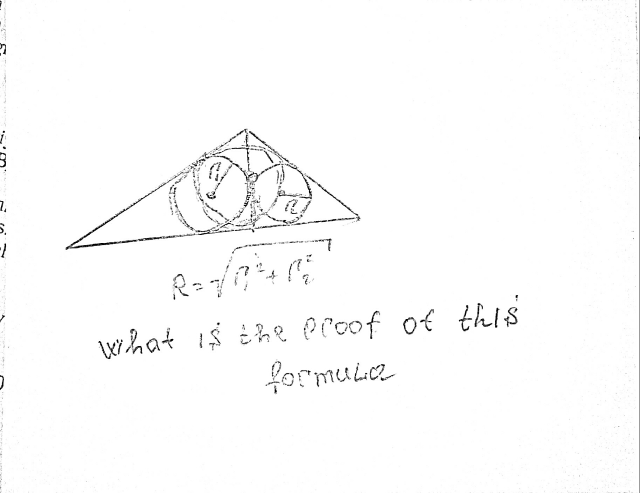
Question Number 50445 Answers: 1 Comments: 1
Question Number 50442 Answers: 1 Comments: 2
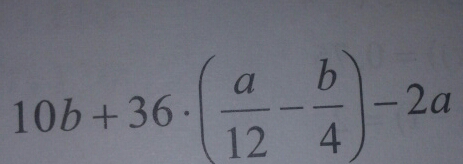
Question Number 50439 Answers: 0 Comments: 1
Question Number 50433 Answers: 0 Comments: 0
Question Number 50432 Answers: 1 Comments: 1
Pg 1591 Pg 1592 Pg 1593 Pg 1594 Pg 1595 Pg 1596 Pg 1597 Pg 1598 Pg 1599 Pg 1600
