
AllQuestion and Answers: Page 1591
Question Number 51287 Answers: 1 Comments: 0

Question Number 51286 Answers: 1 Comments: 0

Question Number 51284 Answers: 1 Comments: 1
Question Number 51279 Answers: 1 Comments: 1
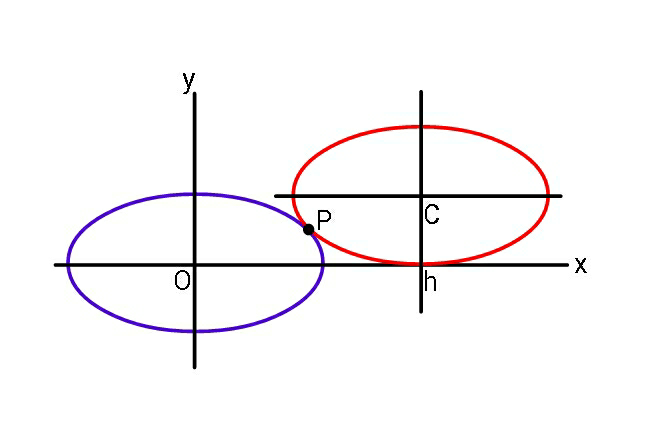
Question Number 51271 Answers: 1 Comments: 0
Question Number 51269 Answers: 1 Comments: 0
Question Number 51263 Answers: 1 Comments: 0
Question Number 51250 Answers: 1 Comments: 0
Question Number 51248 Answers: 1 Comments: 0
Question Number 51245 Answers: 2 Comments: 0

Question Number 51228 Answers: 1 Comments: 1

Question Number 51227 Answers: 1 Comments: 4
Question Number 51220 Answers: 1 Comments: 1
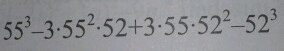
Question Number 51218 Answers: 0 Comments: 0
Question Number 51217 Answers: 0 Comments: 0
Question Number 51216 Answers: 1 Comments: 0
Question Number 51215 Answers: 1 Comments: 0
$$\int_{\mathrm{0}} ^{\pi} {e}^{\left(\mathrm{1}+{i}\right){x}} {dx}=... \\ $$
Question Number 51199 Answers: 0 Comments: 0

Question Number 51236 Answers: 2 Comments: 0
Question Number 51235 Answers: 2 Comments: 0
Question Number 51190 Answers: 0 Comments: 0
Question Number 51188 Answers: 0 Comments: 0
$${find}\:\:\int\:\:\:\:\:\frac{{cos}^{\mathrm{2}} {x}}{{cosx}\:+\mathrm{2}{sinx}}{dx} \\ $$
Question Number 51186 Answers: 1 Comments: 1
Question Number 51185 Answers: 0 Comments: 1
Question Number 51181 Answers: 2 Comments: 1

Question Number 51174 Answers: 0 Comments: 7
Pg 1586 Pg 1587 Pg 1588 Pg 1589 Pg 1590 Pg 1591 Pg 1592 Pg 1593 Pg 1594 Pg 1595
