Question and Answers Forum

AllQuestion and Answers: Page 1579

Question Number 52498 Answers: 1 Comments: 1

Let z is complex number and satisfy z^(2017) = 1, z ≠ 1 Find (1 + z)(1 + z^2 )(1 + z^3 )…(1 + z^(2016) )

$$\mathrm{Let}\:{z}\:\mathrm{is}\:\mathrm{complex}\:\mathrm{number}\:\mathrm{and}\:\mathrm{satisfy}\:{z}^{\mathrm{2017}} \:=\:\mathrm{1},\:\:{z}\:\neq\:\mathrm{1} \\ $$$$\mathrm{Find}\:\left(\mathrm{1}\:+\:{z}\right)\left(\mathrm{1}\:+\:{z}^{\mathrm{2}} \right)\left(\mathrm{1}\:+\:{z}^{\mathrm{3}} \right)\ldots\left(\mathrm{1}\:+\:{z}^{\mathrm{2016}} \right) \\ $$

Question Number 52496 Answers: 2 Comments: 0

How does Evaporation occur and why does it cause Cooling

$${How}\:{does}\:{Evaporation} \\ $$$${occur}\:{and}\:{why}\:{does}\:{it}\: \\ $$$${cause}\:{Cooling} \\ $$

Question Number 52490 Answers: 2 Comments: 1

Question Number 52487 Answers: 0 Comments: 13

Question Number 52484 Answers: 2 Comments: 0

∫ ((cos x − x sin x)/(x cos x)) dx

$$\int\:\:\frac{\mathrm{cos}\:\mathrm{x}\:−\:\mathrm{x}\:\mathrm{sin}\:\mathrm{x}}{\mathrm{x}\:\mathrm{cos}\:\mathrm{x}}\:\:\mathrm{dx} \\ $$

Question Number 52482 Answers: 0 Comments: 2

find the value or ∫_0 ^∞ ((arctan(x^2 ))/(1+x^4 ))dx .

$${find}\:{the}\:{value}\:{or}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{arctan}\left({x}^{\mathrm{2}} \right)}{\mathrm{1}+{x}^{\mathrm{4}} }{dx}\:. \\ $$

Question Number 52470 Answers: 1 Comments: 1

Question Number 52459 Answers: 0 Comments: 2

let f(α)=∫_0 ^1 ((ln(1+iαx))/(1+x^2 ))dx 1)determine a explicit form of f(α) 2) calculate ∫_0 ^1 ((ln(1+ix))/(1+x^2 ))dx and ∫_0 ^1 ((ln(1+2ix))/(1+x^2 ))dx.

$${let}\:{f}\left(\alpha\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{ln}\left(\mathrm{1}+{i}\alpha{x}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$$\left.\mathrm{1}\right){determine}\:{a}\:{explicit}\:{form}\:{of}\:{f}\left(\alpha\right) \\ $$$$\left.\mathrm{2}\right)\:{calculate}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{ln}\left(\mathrm{1}+{ix}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\:{and}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{ln}\left(\mathrm{1}+\mathrm{2}{ix}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}. \\ $$

Question Number 52457 Answers: 1 Comments: 0

Two radioactive elements A and B has half lives of 100 and 50years. Samples of A and B initial contains equal numbers of atoms.What is the ratio of the remaining atoms of A to that of B after 200years?

$${Two}\:{radioactive}\:{elements}\:{A}\:{and}\:{B} \\ $$$${has}\:{half}\:{lives}\:{of}\:\mathrm{100}\:{and}\:\mathrm{50}{years}. \\ $$$${Samples}\:{of}\:{A}\:{and}\:{B}\:{initial}\:{contains} \\ $$$${equal}\:{numbers}\:{of}\:{atoms}.{What}\:{is} \\ $$$${the}\:{ratio}\:{of}\:{the}\:{remaining}\:{atoms} \\ $$$${of}\:{A}\:{to}\:{that}\:{of}\:{B}\:{after}\:\mathrm{200}{years}? \\ $$

Question Number 52450 Answers: 0 Comments: 0

let P(x)=(1+ix −x^2 )^n −1 find roots of P(x) and factorize P(x)inside C(x).

$${let}\:{P}\left({x}\right)=\left(\mathrm{1}+{ix}\:−{x}^{\mathrm{2}} \right)^{{n}} −\mathrm{1} \\ $$$${find}\:{roots}\:{of}\:\:{P}\left({x}\right)\:{and}\:{factorize}\:{P}\left({x}\right){inside}\:{C}\left({x}\right). \\ $$

Question Number 52468 Answers: 2 Comments: 4

Question Number 52466 Answers: 1 Comments: 1

Question Number 52433 Answers: 0 Comments: 4

Question Number 52428 Answers: 0 Comments: 7

Question Number 52426 Answers: 2 Comments: 1

Question Number 52421 Answers: 0 Comments: 2

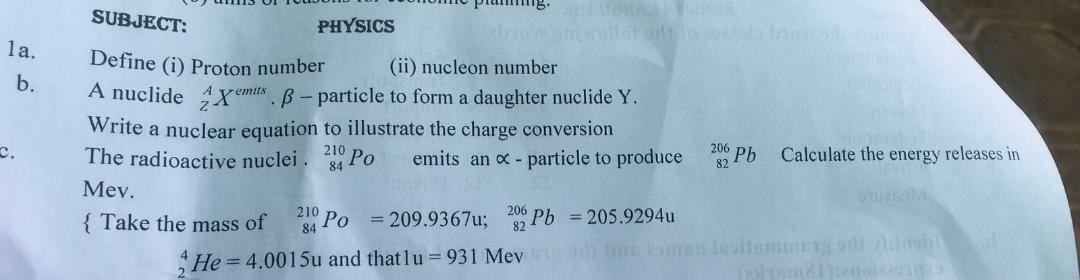
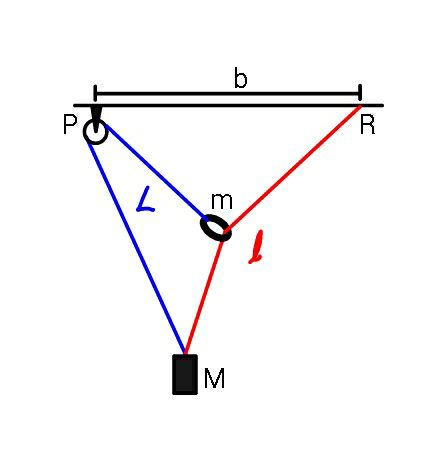
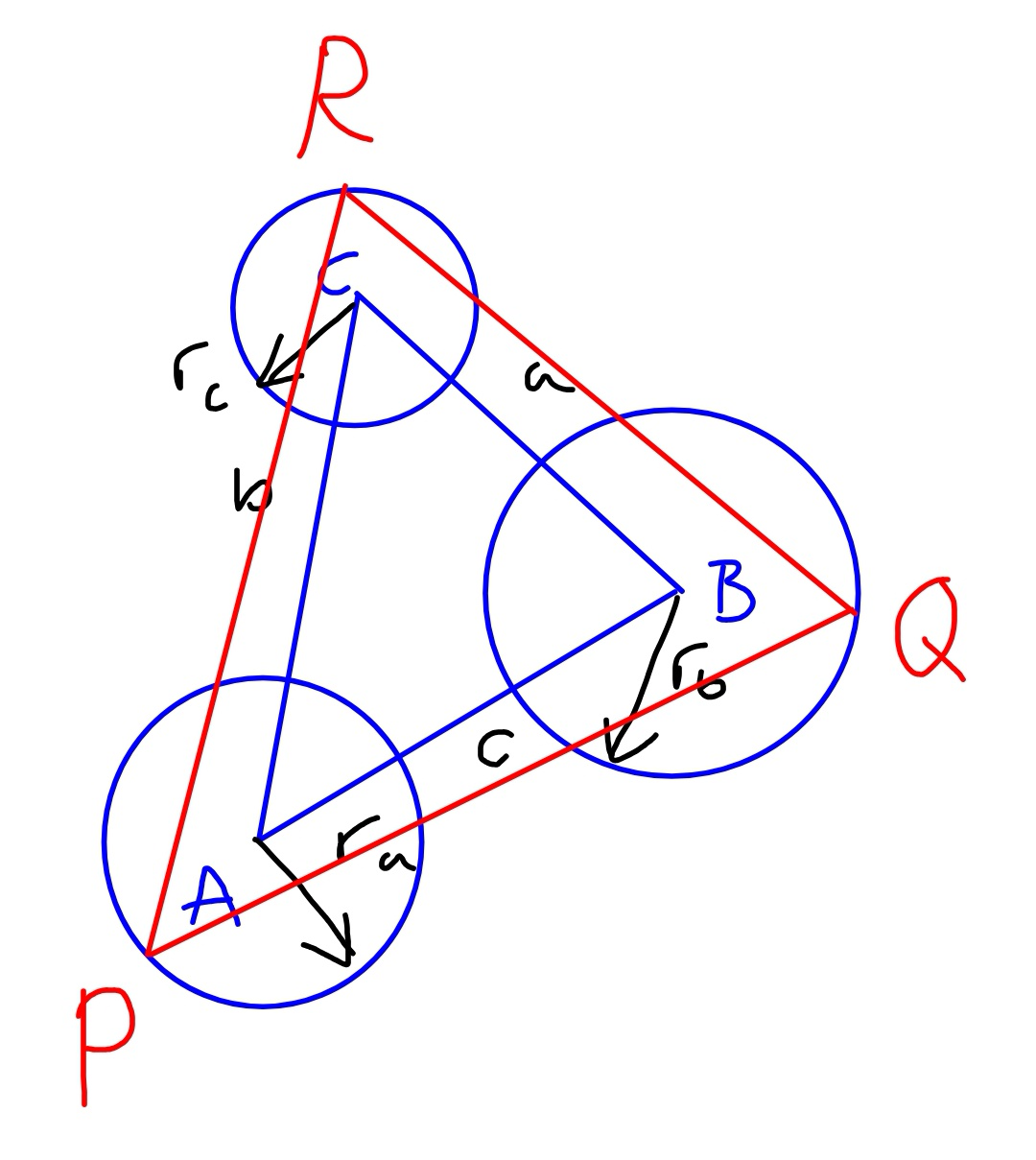
Question Number 52418 Answers: 0 Comments: 1

find the value of ∫_0 ^∞ ((arctan(x))/(1+x^4 )) dx

$${find}\:{the}\:{value}\:{of}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{arctan}\left({x}\right)}{\mathrm{1}+{x}^{\mathrm{4}} }\:{dx} \\ $$

Question Number 52412 Answers: 0 Comments: 3

Question Number 52409 Answers: 1 Comments: 1

Question Number 52406 Answers: 2 Comments: 0

Find the cube root of 26 + 5(√3)

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{cube}\:\mathrm{root}\:\mathrm{of}\:\:\:\:\:\mathrm{26}\:+\:\mathrm{5}\sqrt{\mathrm{3}} \\ $$

Question Number 52397 Answers: 0 Comments: 1

Question Number 52392 Answers: 0 Comments: 0

Question Number 52391 Answers: 1 Comments: 1

2299/(7x+20)=11 sir could you help me?

$$\mathrm{2299}/\left(\mathrm{7x}+\mathrm{20}\right)=\mathrm{11}\:\:\:\: \\ $$$$\mathrm{sir}\:\mathrm{could}\:\mathrm{you}\:\mathrm{help}\:\mathrm{me}? \\ $$

Question Number 52381 Answers: 2 Comments: 0

If all the words with or without meaning are written using the letters of the word QUEEN and are arranged as in English dictionary.What is the position of the word QUEEN? a)44th b)45th c)46th d)47th

$${If}\:{all}\:{the}\:{words}\:{with}\:{or}\:{without} \\ $$$${meaning}\:{are}\:{written}\:{using}\:{the} \\ $$$${letters}\:{of}\:{the}\:{word}\:{QUEEN}\:{and} \\ $$$${are}\:{arranged}\:{as}\:{in}\:{English} \\ $$$${dictionary}.{What}\:{is}\:{the}\:{position} \\ $$$${of}\:{the}\:{word}\:{QUEEN}? \\ $$$$\left.{a}\left.\right)\left.\mathrm{4}\left.\mathrm{4}{th}\:{b}\right)\mathrm{45}{th}\:{c}\right)\mathrm{46}{th}\:{d}\right)\mathrm{47}{th} \\ $$

Question Number 52379 Answers: 1 Comments: 0

The sum of the digits in the unit place of all four digit numbers formed using the numbers 3 4 5 andL 6 without repetition is a)432 b)108 c)36 d)18

$${The}\:{sum}\:{of}\:{the}\:{digits}\:{in}\:{the}\:{unit} \\ $$$${place}\:{of}\:{all}\:{four}\:{digit}\:{numbers} \\ $$$${formed}\:{using}\:{the}\:{numbers}\:\mathrm{3}\:\mathrm{4}\:\mathrm{5}\:{and}\mathscr{L} \\ $$$$\mathrm{6}\:{without}\:{repetition}\:{is} \\ $$$$\left.{a}\left.\right)\left.\mathrm{4}\left.\mathrm{32}\:{b}\right)\mathrm{108}\:{c}\right)\mathrm{36}\:{d}\right)\mathrm{18} \\ $$

Question Number 52377 Answers: 0 Comments: 3

An iceberg is floating in sea water. The density of ice is 0.92g/cm^3 and that of sea water is 1.02g/cm^3 . What % of ice will be below the water?

$${An}\:{iceberg}\:{is}\:{floating}\:{in}\:{sea}\:{water}. \\ $$$${The}\:{density}\:{of}\:{ice}\:{is}\:\mathrm{0}.\mathrm{92}{g}/{cm}^{\mathrm{3}} \\ $$$${and}\:{that}\:{of}\:{sea}\:{water}\:{is}\:\mathrm{1}.\mathrm{02}{g}/{cm}^{\mathrm{3}} . \\ $$$${What}\:\%\:{of}\:{ice}\:{will}\:\:{be}\:{below}\:{the} \\ $$$${water}? \\ $$

Pg 1574 Pg 1575 Pg 1576 Pg 1577 Pg 1578 Pg 1579 Pg 1580 Pg 1581 Pg 1582 Pg 1583

Contact: info@tinkutara.com