
AllQuestion and Answers: Page 1568
Question Number 54416 Answers: 0 Comments: 0
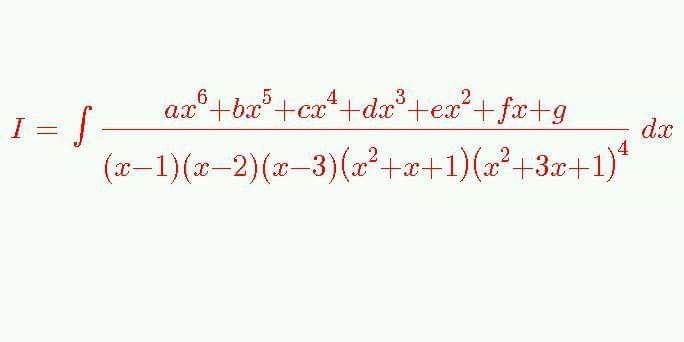
Question Number 54413 Answers: 0 Comments: 8
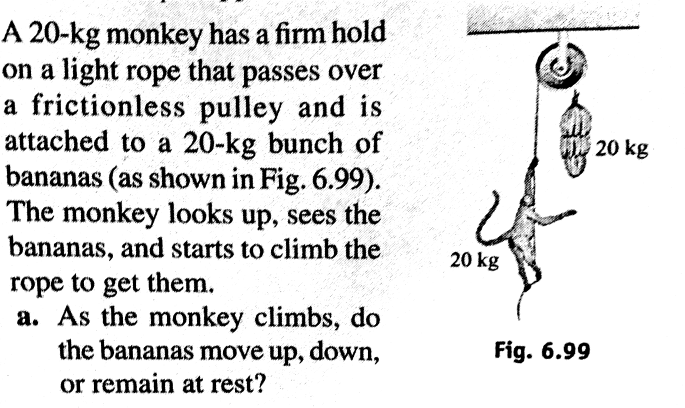
Question Number 54409 Answers: 2 Comments: 1
Question Number 54396 Answers: 1 Comments: 1
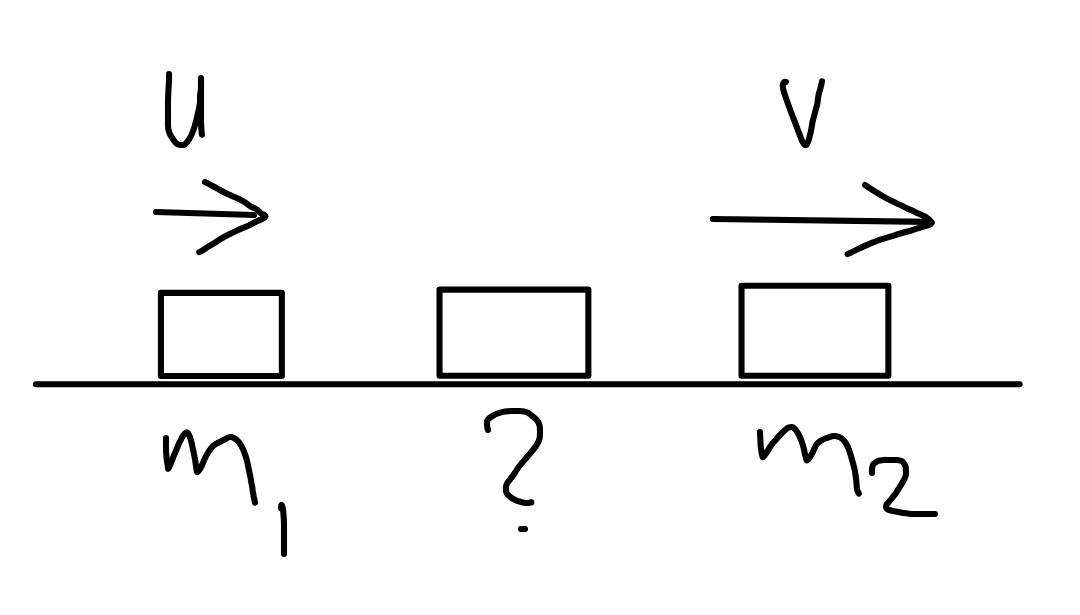
Question Number 54388 Answers: 0 Comments: 0
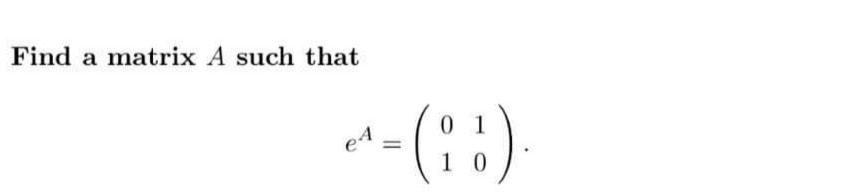
Question Number 54378 Answers: 0 Comments: 3
Question Number 54377 Answers: 0 Comments: 0
Question Number 54376 Answers: 3 Comments: 3
Question Number 54374 Answers: 0 Comments: 1
Question Number 54372 Answers: 1 Comments: 3
Question Number 54371 Answers: 1 Comments: 1
Question Number 54369 Answers: 0 Comments: 2
Question Number 54367 Answers: 1 Comments: 1
Question Number 54364 Answers: 1 Comments: 0
Question Number 54360 Answers: 2 Comments: 1

Question Number 54357 Answers: 2 Comments: 1

Question Number 54353 Answers: 0 Comments: 1
Question Number 54341 Answers: 1 Comments: 0

Question Number 58312 Answers: 0 Comments: 4
Question Number 58313 Answers: 2 Comments: 2
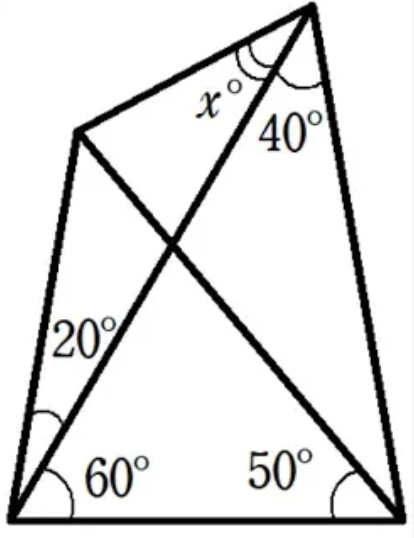
Question Number 54334 Answers: 1 Comments: 1

Question Number 54322 Answers: 3 Comments: 0

Question Number 54312 Answers: 1 Comments: 2
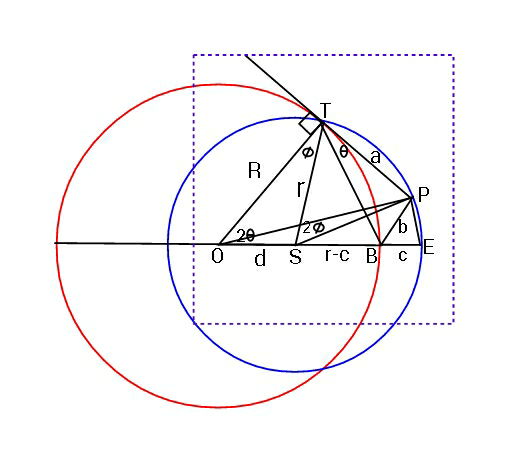
Question Number 54289 Answers: 2 Comments: 5

Question Number 54286 Answers: 2 Comments: 2

Question Number 54281 Answers: 0 Comments: 1

Pg 1563 Pg 1564 Pg 1565 Pg 1566 Pg 1567 Pg 1568 Pg 1569 Pg 1570 Pg 1571 Pg 1572
