
AllQuestion and Answers: Page 1567
Question Number 54537 Answers: 1 Comments: 2
Question Number 54536 Answers: 1 Comments: 0
Question Number 54526 Answers: 1 Comments: 1
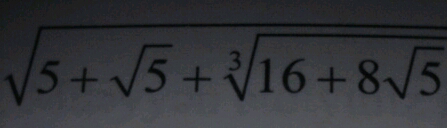
Question Number 54517 Answers: 2 Comments: 0
Question Number 54529 Answers: 1 Comments: 2
$$\int\mathrm{5cos}\:{x}−\mathrm{4sin}\:{x}/\mathrm{2cos}\:{x}+\mathrm{sin}\:{x}\:{dx} \\ $$
Question Number 54513 Answers: 1 Comments: 0
Question Number 54506 Answers: 3 Comments: 0
Question Number 54504 Answers: 1 Comments: 0
Question Number 54502 Answers: 0 Comments: 5
Question Number 54480 Answers: 2 Comments: 0
Question Number 54481 Answers: 1 Comments: 1

Question Number 54473 Answers: 1 Comments: 0
Question Number 54472 Answers: 1 Comments: 0
Question Number 54468 Answers: 0 Comments: 0
Question Number 54466 Answers: 1 Comments: 1
Question Number 54462 Answers: 1 Comments: 1

Question Number 54460 Answers: 1 Comments: 0
Question Number 54457 Answers: 0 Comments: 0

Question Number 54447 Answers: 2 Comments: 1

Question Number 54487 Answers: 0 Comments: 0

Question Number 54422 Answers: 1 Comments: 4
Question Number 54421 Answers: 2 Comments: 2
Question Number 54420 Answers: 1 Comments: 0
Question Number 54419 Answers: 1 Comments: 0
Question Number 54418 Answers: 1 Comments: 0
Question Number 54417 Answers: 0 Comments: 0
Pg 1562 Pg 1563 Pg 1564 Pg 1565 Pg 1566 Pg 1567 Pg 1568 Pg 1569 Pg 1570 Pg 1571
