
AllQuestion and Answers: Page 1566
Question Number 54659 Answers: 1 Comments: 2

Question Number 54658 Answers: 0 Comments: 0

Question Number 54647 Answers: 0 Comments: 3
Question Number 54646 Answers: 2 Comments: 0
Question Number 54644 Answers: 1 Comments: 0
Question Number 54641 Answers: 0 Comments: 1
Question Number 54626 Answers: 2 Comments: 0
Question Number 54616 Answers: 2 Comments: 0
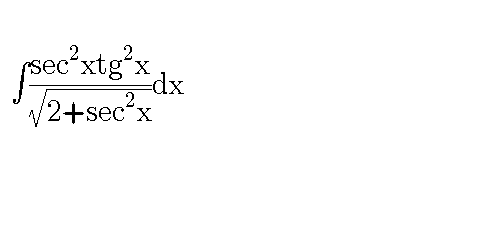
Question Number 54607 Answers: 1 Comments: 2
Question Number 54603 Answers: 1 Comments: 0
Question Number 54602 Answers: 0 Comments: 1
Question Number 54600 Answers: 2 Comments: 2
Question Number 54595 Answers: 0 Comments: 3
Question Number 54588 Answers: 1 Comments: 0
Question Number 54586 Answers: 1 Comments: 0
Question Number 54585 Answers: 1 Comments: 1
Question Number 54584 Answers: 2 Comments: 0

Question Number 54582 Answers: 0 Comments: 1
Question Number 54578 Answers: 1 Comments: 1
Question Number 54573 Answers: 0 Comments: 1
Question Number 54566 Answers: 0 Comments: 3
Question Number 54563 Answers: 1 Comments: 1
Question Number 54562 Answers: 1 Comments: 0

Question Number 54556 Answers: 0 Comments: 4
Question Number 54543 Answers: 1 Comments: 1
Question Number 54541 Answers: 1 Comments: 0
Pg 1561 Pg 1562 Pg 1563 Pg 1564 Pg 1565 Pg 1566 Pg 1567 Pg 1568 Pg 1569 Pg 1570
