
AllQuestion and Answers: Page 1565
Question Number 54322 Answers: 3 Comments: 0

Question Number 54312 Answers: 1 Comments: 2
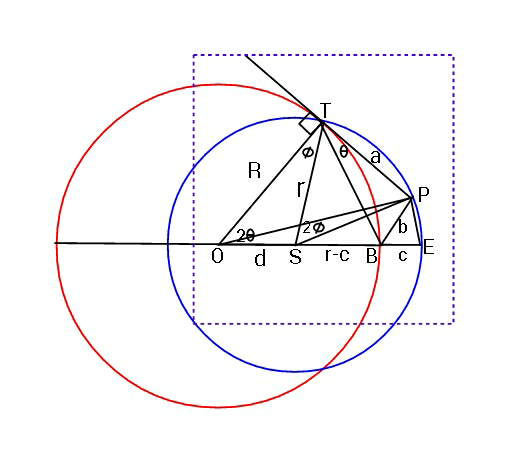
Question Number 54289 Answers: 2 Comments: 5

Question Number 54286 Answers: 2 Comments: 2

Question Number 54281 Answers: 0 Comments: 1

Question Number 54278 Answers: 0 Comments: 4
Question Number 54271 Answers: 1 Comments: 1
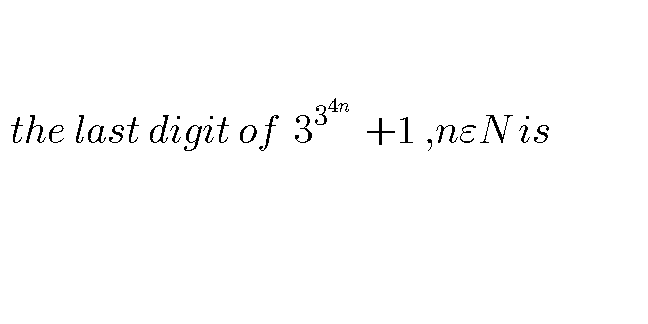
Question Number 54270 Answers: 2 Comments: 0
Question Number 54268 Answers: 0 Comments: 1

Question Number 54259 Answers: 1 Comments: 1

Question Number 54258 Answers: 0 Comments: 1

Question Number 54273 Answers: 2 Comments: 0

Question Number 54248 Answers: 2 Comments: 1

Question Number 54242 Answers: 2 Comments: 0
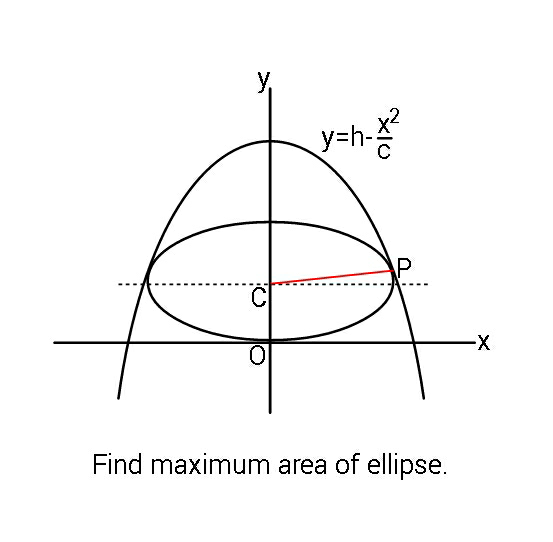
Question Number 54240 Answers: 1 Comments: 1

Question Number 54239 Answers: 1 Comments: 0
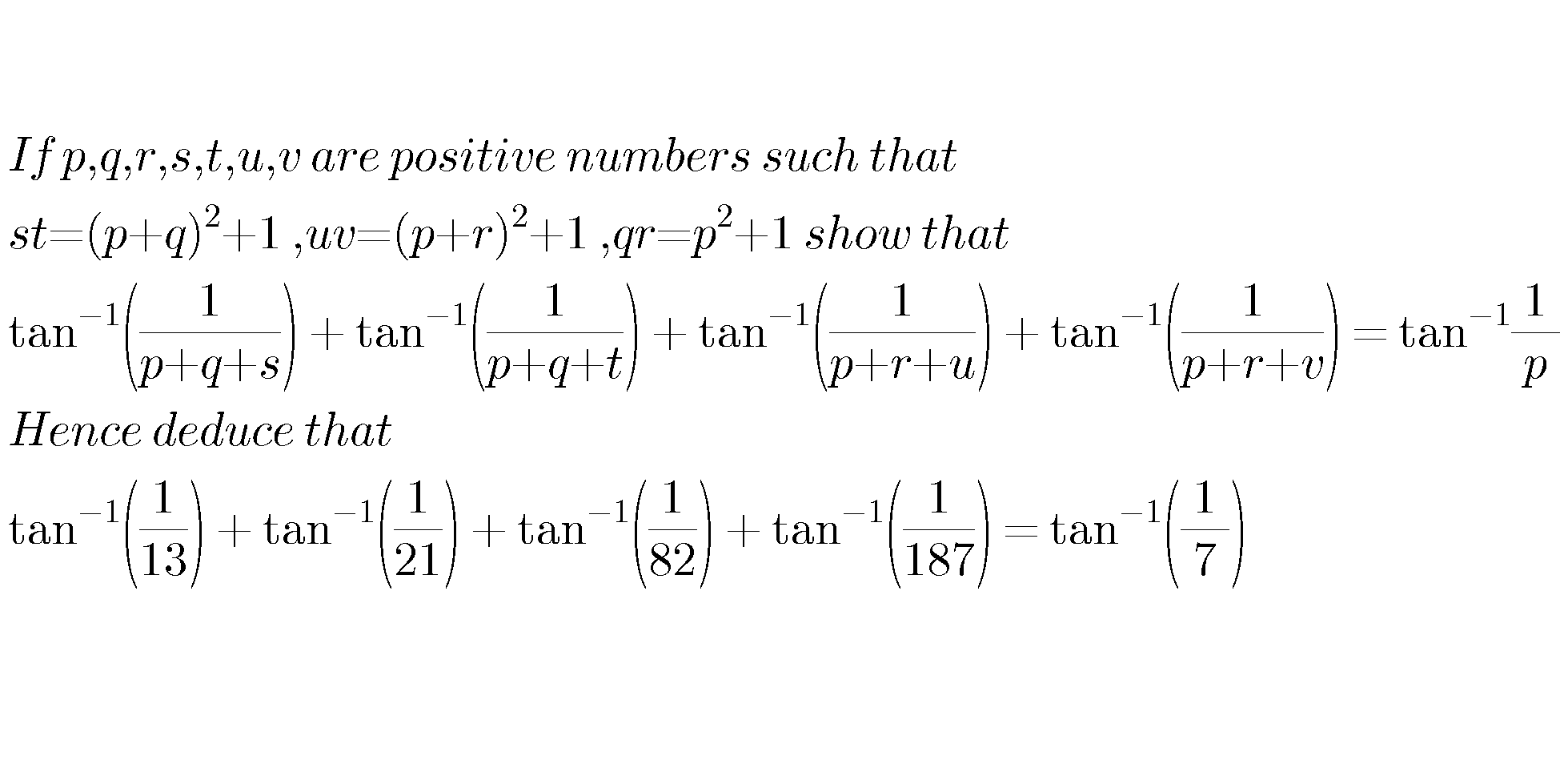
Question Number 54229 Answers: 1 Comments: 1
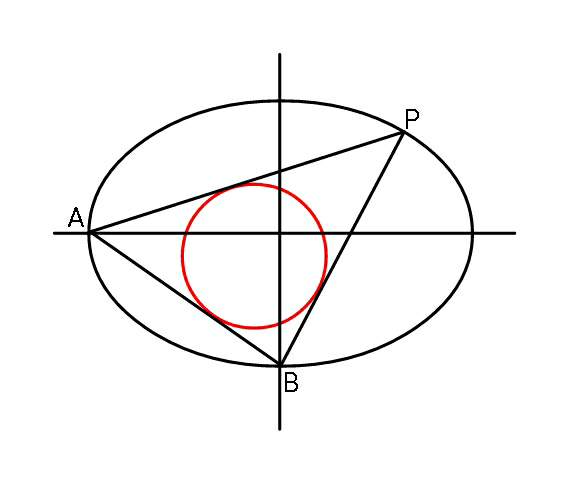
Question Number 54226 Answers: 0 Comments: 4

Question Number 54224 Answers: 2 Comments: 4
Question Number 54219 Answers: 1 Comments: 0
Question Number 54209 Answers: 2 Comments: 0

Question Number 54206 Answers: 1 Comments: 2
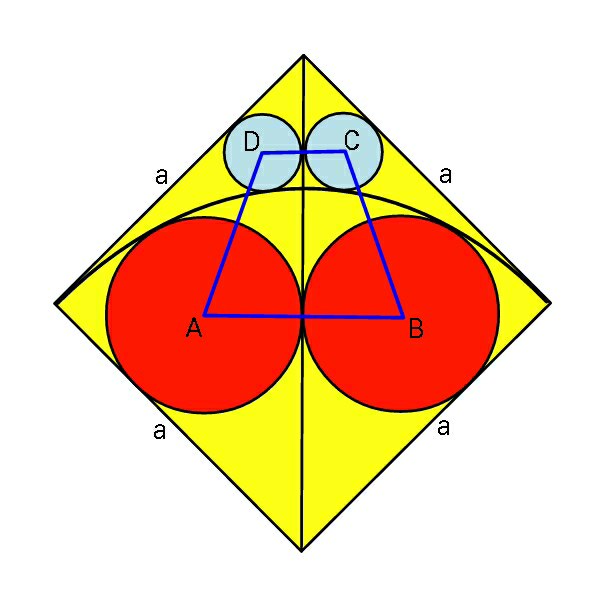
Question Number 54194 Answers: 1 Comments: 1

Question Number 54199 Answers: 0 Comments: 0
Question Number 54176 Answers: 0 Comments: 0
$${what}\:{is}\:{the}\:{integral}\:{vslue}\:{of}\:\int{x}!{dx} \\ $$
Question Number 54170 Answers: 1 Comments: 1
Pg 1560 Pg 1561 Pg 1562 Pg 1563 Pg 1564 Pg 1565 Pg 1566 Pg 1567 Pg 1568 Pg 1569
