Question and Answers Forum

AllQuestion and Answers: Page 1564

Question Number 54901 Answers: 1 Comments: 1

Question Number 54897 Answers: 2 Comments: 1

Find value of n so 120 ∣ 5n(n^2 −1)

$$\mathrm{Find}\:\mathrm{value}\:\mathrm{of}\:{n}\:\mathrm{so}\:\mathrm{120}\:\mid\:\mathrm{5}{n}\left({n}^{\mathrm{2}} −\mathrm{1}\right) \\ $$

Question Number 54896 Answers: 1 Comments: 1

∫(√)(x2+2x+2)

$$\int\sqrt{}\left({x}\mathrm{2}+\mathrm{2}{x}+\mathrm{2}\right) \\ $$

Question Number 54880 Answers: 2 Comments: 0

If x^2 −y^2 =a^2 find (d^2 y/dx^2 ) if a is constant.

$${If}\:{x}^{\mathrm{2}} −{y}^{\mathrm{2}} ={a}^{\mathrm{2}} \:\:{find}\:\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }\:{if}\:{a}\:{is} \\ $$$${constant}. \\ $$

Question Number 54876 Answers: 1 Comments: 1

find the coefficientof x^2 in the binomial expansion of (x^2 +(2/x))^4

$$\mathrm{find}\:\mathrm{the}\:\mathrm{coefficientof}\:\mathrm{x}^{\mathrm{2}} \:\mathrm{in}\:\mathrm{the}\:\mathrm{binomial} \\ $$$$\mathrm{expansion}\:\mathrm{of}\:\left(\mathrm{x}^{\mathrm{2}} +\frac{\mathrm{2}}{\mathrm{x}}\right)^{\mathrm{4}} \\ $$

Question Number 54875 Answers: 2 Comments: 0

Given that((log(3x+1)^(2x−1) )/(log(3x+1)))=5,find the value of x.

$$\mathrm{Given}\:\mathrm{that}\frac{\mathrm{log}\left(\mathrm{3x}+\mathrm{1}\right)^{\mathrm{2x}−\mathrm{1}} }{\mathrm{log}\left(\mathrm{3x}+\mathrm{1}\right)}=\mathrm{5},\mathrm{find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{x}. \\ $$

Question Number 54869 Answers: 1 Comments: 0

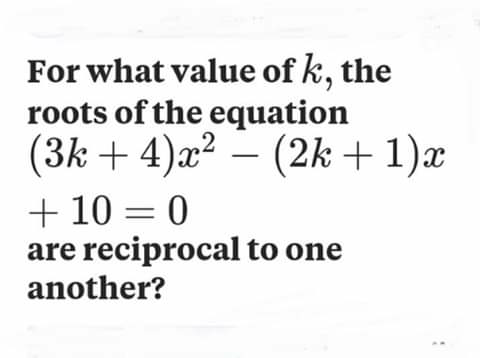
Question Number 54868 Answers: 0 Comments: 1

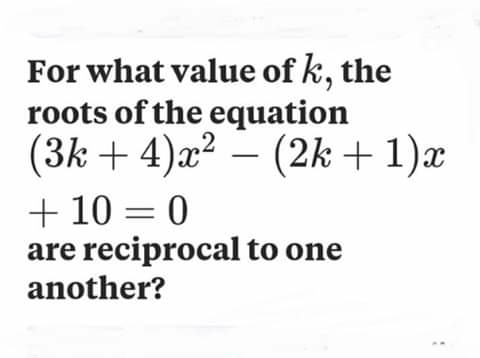
Question Number 54860 Answers: 1 Comments: 1

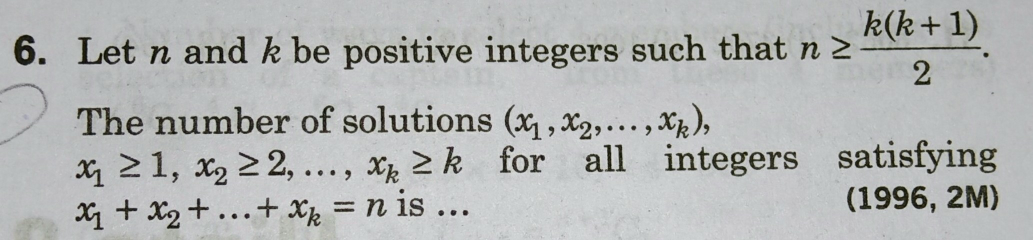
Question Number 54858 Answers: 2 Comments: 0

(Q1) The expansion (x−(1/(3x)))^(12) (i) find the term independent of x (ii) find the term x^4 (Q2) There are some nut in a bag. when 2 ounces of peanut are added to the mixture, the percentage of peanut becomes 20% . Richard added 2 ounces of cashew to the mixture and the percentage of cashew nut was 33.33% . find the percentage of cashew nut that were there initially. please sir help

$$\left({Q}\mathrm{1}\right)\:{The}\:{expansion}\:\left({x}−\frac{\mathrm{1}}{\mathrm{3}{x}}\right)^{\mathrm{12}} \\ $$$$\left({i}\right)\:{find}\:{the}\:{term}\:{independent}\:{of}\:{x} \\ $$$$\left({ii}\right)\:{find}\:{the}\:{term}\:{x}^{\mathrm{4}} \\ $$$$\left({Q}\mathrm{2}\right)\:{There}\:{are}\:{some}\:{nut}\:{in}\:{a}\:{bag}.\:{when} \\ $$$$\:\mathrm{2}\:{ounces}\:{of}\:{peanut}\:{are}\:{added}\:{to}\:{the} \\ $$$${mixture},\:{the}\:{percentage}\:{of}\:{peanut}\: \\ $$$${becomes}\:\mathrm{20\%}\:.\:{Richard}\:\:{added}\:\:\mathrm{2}\: \\ $$$${ounces}\:{of}\:{cashew}\:{to}\:{the}\:{mixture}\:{and} \\ $$$${the}\:{percentage}\:{of}\:{cashew}\:{nut}\:{was}\: \\ $$$$\mathrm{33}.\mathrm{33\%}\:.\:{find}\:{the}\:{percentage}\:{of}\: \\ $$$${cashew}\:{nut}\:{that}\:{were}\:{there}\:{initially}. \\ $$$${please}\:{sir}\:{help} \\ $$

Question Number 54857 Answers: 1 Comments: 0

Question Number 54856 Answers: 1 Comments: 2

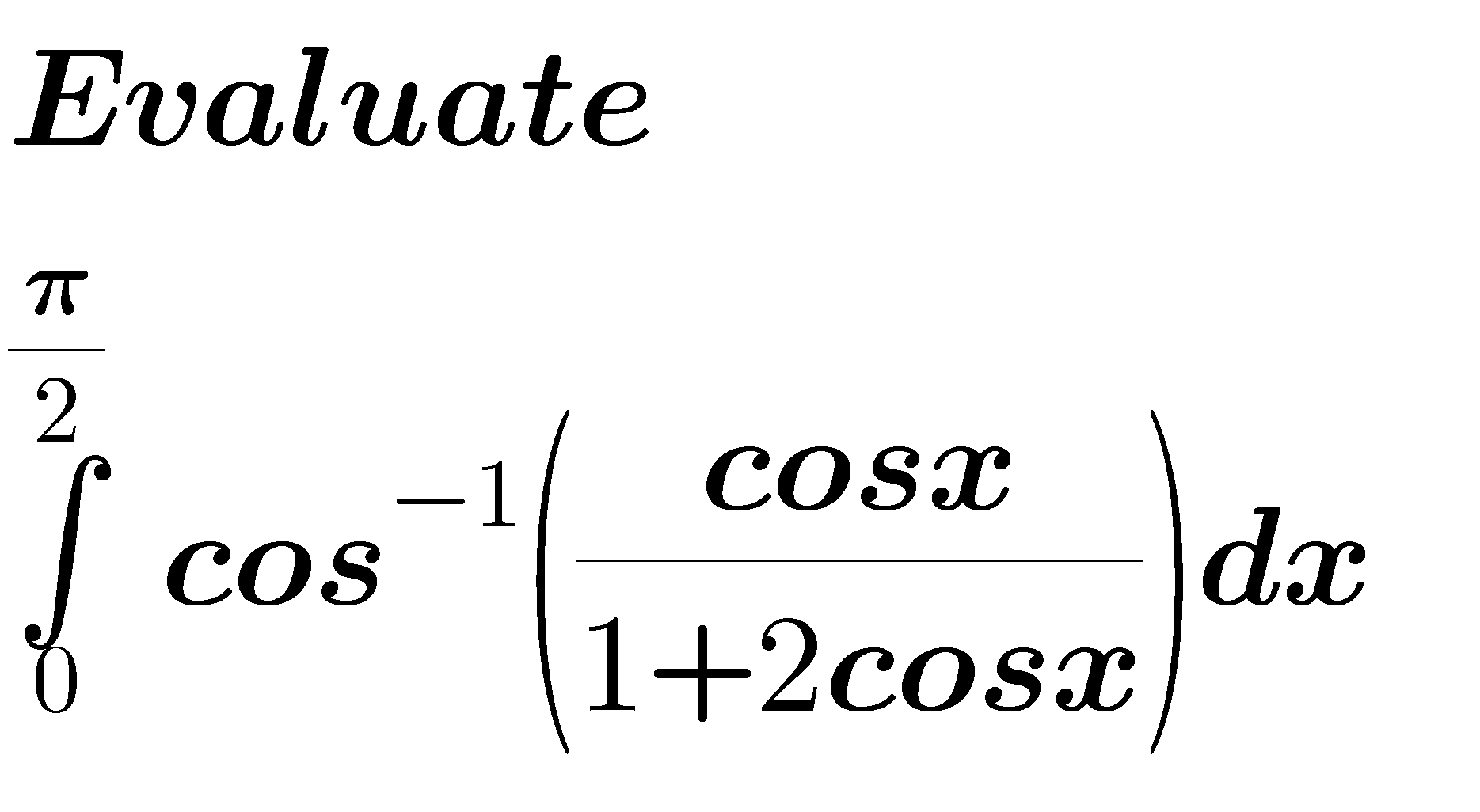
Question Number 54841 Answers: 1 Comments: 0

Question Number 54830 Answers: 0 Comments: 1

let V_n = ∫_0 ^∞ ((cos(nx))/(n +x^2 ))dx with n integr nstural not 0 . 1) calculate V_n 2)calculate lim_(n→+∞) nV_n 3) calculate the sum Σ_(n=0) ^∞ V_n

$${let}\:{V}_{{n}} =\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{cos}\left({nx}\right)}{{n}\:+{x}^{\mathrm{2}} }{dx}\:\:\:{with}\:{n}\:{integr}\:{nstural}\:{not}\:\mathrm{0}\:. \\ $$$$\left.\mathrm{1}\right)\:{calculate}\:{V}_{{n}} \\ $$$$\left.\mathrm{2}\right){calculate}\:{lim}_{{n}\rightarrow+\infty} {nV}_{{n}} \\ $$$$\left.\mathrm{3}\right)\:{calculate}\:{the}\:{sum}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:{V}_{{n}} \\ $$

Question Number 54827 Answers: 0 Comments: 0

logx^2 +log_2 (x−6)=3 solve for x

$$\mathrm{logx}^{\mathrm{2}} +\mathrm{log}_{\mathrm{2}} \left(\mathrm{x}−\mathrm{6}\right)=\mathrm{3} \\ $$$$\mathrm{solve}\:\mathrm{for}\:\mathrm{x} \\ $$

Question Number 54826 Answers: 4 Comments: 5

1) ∫_0 ^( 1) ((1−x^7 )^(1/4) −(1−x^4 )^(1/7) )dx = ? 2) If f(x)=x^3 +3x+4 then the value of ∫_(−1) ^( 1) f(x)dx + ∫_0 ^( 4) f^( −1) (x)dx = ? 3) ∫_(−π) ^( π) (1+cosx+cos2x+....+cos13x)(1+sinx+...+sin13x)dx=? 4) ∫_0 ^( 2) ((√(x^3 +1)) + (x^2 +2x)^(1/3) )dx =? (This time func. are not inverse of each other,right ?)

$$\left.\mathrm{1}\right)\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \:\left(\left(\mathrm{1}−{x}^{\mathrm{7}} \right)^{\frac{\mathrm{1}}{\mathrm{4}}} −\left(\mathrm{1}−{x}^{\mathrm{4}} \right)^{\frac{\mathrm{1}}{\mathrm{7}}} \right){dx}\:=\:? \\ $$$$\left.\mathrm{2}\right)\:{If}\:{f}\left({x}\right)={x}^{\mathrm{3}} +\mathrm{3}{x}+\mathrm{4}\:{then}\:{the}\:{value}\:{of} \\ $$$$\:\int_{−\mathrm{1}} ^{\:\mathrm{1}} {f}\left({x}\right){dx}\:+\:\int_{\mathrm{0}} ^{\:\mathrm{4}} {f}^{\:−\mathrm{1}} \left({x}\right){dx}\:=\:? \\ $$$$\left.\mathrm{3}\right)\:\int_{−\pi} ^{\:\pi} \left(\mathrm{1}+{cosx}+{cos}\mathrm{2}{x}+....+{cos}\mathrm{13}{x}\right)\left(\mathrm{1}+{sinx}+...+{sin}\mathrm{13}{x}\right){dx}=? \\ $$$$\left.\mathrm{4}\right)\:\int_{\mathrm{0}} ^{\:\mathrm{2}} \:\left(\sqrt{{x}^{\mathrm{3}} +\mathrm{1}}\:+\:\left({x}^{\mathrm{2}} +\mathrm{2}{x}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \:\right){dx}\:=? \\ $$$$\left({This}\:{time}\:{func}.\:{are}\:{not}\:{inverse}\:{of}\:{each}\right. \\ $$$$\left.{other},{right}\:?\right) \\ $$

Question Number 54825 Answers: 1 Comments: 0

Question Number 54808 Answers: 1 Comments: 2

let p(x)=(1+x^2 )(1+x^4 )...(1+x^2^n ) with n integr natural 1) find a simple form of p(x) 2) find roots of p(x)and decompose p(x) inside C[x] 3)calculate ∫_0 ^1 p(x)dx 4) decompose the fraction F(x)=(1/(p(x))) .

$${let}\:{p}\left({x}\right)=\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\left(\mathrm{1}+{x}^{\mathrm{4}} \right)...\left(\mathrm{1}+{x}^{\mathrm{2}^{{n}} } \right) \\ $$$${with}\:{n}\:{integr}\:{natural} \\ $$$$\left.\mathrm{1}\right)\:{find}\:{a}\:{simple}\:{form}\:{of}\:{p}\left({x}\right) \\ $$$$\left.\mathrm{2}\right)\:{find}\:{roots}\:{of}\:{p}\left({x}\right){and}\:{decompose} \\ $$$${p}\left({x}\right)\:{inside}\:{C}\left[{x}\right] \\ $$$$\left.\mathrm{3}\right){calculate}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{p}\left({x}\right){dx} \\ $$$$\left.\mathrm{4}\right)\:{decompose}\:{the}\:{fraction} \\ $$$${F}\left({x}\right)=\frac{\mathrm{1}}{{p}\left({x}\right)}\:. \\ $$

Question Number 54797 Answers: 1 Comments: 0

∫ (√( x + (√( x + (√(x + (√( .....)))))))) dx = ?

$$ \\ $$$$ \\ $$$$\:\:\:\int\:\:\sqrt{\:\boldsymbol{{x}}\:+\:\sqrt{\:\boldsymbol{{x}}\:+\:\sqrt{\boldsymbol{{x}}\:+\:\sqrt{\:.....}}}}\:\:\boldsymbol{{dx}}\:\:=\:\:\:? \\ $$$$ \\ $$

Question Number 54821 Answers: 0 Comments: 1

find lim_(n→+∞) ∫_0 ^n ((arctan(nx))/(n^2 +x^2 ))dx

$${find}\:{lim}_{{n}\rightarrow+\infty} \:\:\:\int_{\mathrm{0}} ^{{n}} \:\:\:\frac{{arctan}\left({nx}\right)}{{n}^{\mathrm{2}} \:+{x}^{\mathrm{2}} }{dx} \\ $$

Question Number 54790 Answers: 3 Comments: 2

differenciatethefollowing i)x^x +(sinx)^(lnx) = ii)sin^(−1) (tanhx)= iii)(√(1+x^2 /1−x^2 =))

$${differenciatethefollowing} \\ $$$$\left.{i}\right){x}^{{x}} +\left({sinx}\right)^{{lnx}} = \\ $$$$\left.{ii}\right){sin}^{−\mathrm{1}} \left({tanhx}\right)= \\ $$$$\left.{iii}\right)\sqrt{\mathrm{1}+{x}^{\mathrm{2}} /\mathrm{1}−{x}^{\mathrm{2}} =} \\ $$

Question Number 54788 Answers: 2 Comments: 1

How can cut a right angeled triangle to make a square? how can cut a equilateral triangle to make a rectangle?

Question Number 54787 Answers: 0 Comments: 0

if: (a/((√b)+(√c)))=(b/((√c)+(√d)))=(c/((√d)+(√a)))=(d/((√a)+(√b))) ⇒(a/d)=?

$$\:{if}:\:\:\frac{{a}}{\sqrt{{b}}+\sqrt{{c}}}=\frac{{b}}{\sqrt{{c}}+\sqrt{{d}}}=\frac{{c}}{\sqrt{{d}}+\sqrt{{a}}}=\frac{{d}}{\sqrt{{a}}+\sqrt{{b}}} \\ $$$$\Rightarrow\frac{{a}}{{d}}=? \\ $$

Question Number 54786 Answers: 0 Comments: 5

solve for:a,b,c,d∈R a^2 =b+(√c) b^2 =c+(√d) c^2 =d+(√a) d^2 =a+(√b)

$${solve}\:{for}:{a},{b},{c},{d}\in\boldsymbol{{R}} \\ $$$$\:\:\:\:\:\:{a}^{\mathrm{2}} ={b}+\sqrt{{c}} \\ $$$$\:\:\:\:\:\:{b}^{\mathrm{2}} ={c}+\sqrt{{d}} \\ $$$$\:\:\:\:\:\:{c}^{\mathrm{2}} ={d}+\sqrt{{a}} \\ $$$$\:\:\:\:\:\:{d}^{\mathrm{2}} ={a}+\sqrt{{b}} \\ $$

Question Number 54777 Answers: 0 Comments: 1

let u_n =∫_0 ^∞ ((sin(nx^2 ))/(x^2 +6))dx 1) calculate u_n and lim u_n (n→+∞) 2) find nature of Σ u_n and calaculate it. 3) find nature of Σ u_n ^2

$${let}\:{u}_{{n}} =\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{sin}\left({nx}^{\mathrm{2}} \right)}{{x}^{\mathrm{2}} \:+\mathrm{6}}{dx} \\ $$$$\left.\mathrm{1}\right)\:{calculate}\:\:{u}_{{n}} \:\:\:{and}\:{lim}\:{u}_{{n}} \left({n}\rightarrow+\infty\right) \\ $$$$\left.\mathrm{2}\right)\:{find}\:{nature}\:{of}\:\Sigma\:{u}_{{n}} \:\:\:{and}\:{calaculate}\:{it}. \\ $$$$\left.\mathrm{3}\right)\:{find}\:{nature}\:\:{of}\:\Sigma\:{u}_{{n}} ^{\mathrm{2}} \\ $$

Question Number 54775 Answers: 0 Comments: 2

found something interesting, it was published by Tschirnhaus in 1683 we can reduce x^3 +ax^2 +bx+c=0 (1) to y^3 +py+q=0 (2) and further to z^3 =t (1) is the well known linear substitution y=x+(a/3) → x=y−(a/3) ⇒ y^3 −((a^2 −3b)/3)y+((2a^3 −9ab+27c)/(27))=0 p=−((a^2 −3b)/3) and q=((2a^3 −9ab+27c)/(27)) ⇒ y^3 +py+q=0 (2) quadratic substitution z=y^2 +αy+β → y^2 +αy+(β−z)=0 we could solve this for y and then plug in above... (Tschirnhaus did) but there′s an easier way: we calculate the determinant of the Sylvester Matrix we have (a) 1y^3 +0y^2 +py+q=0 (b) 0y^3 +y^2 +αy+(β−z)=0 the matrix is [(1,0,p,q,0),(0,1,0,p,q),(0,1,α,(β−z),0),(0,0,1,α,(β−z)),(1,α,(β−z),0,0) ] the determinant is −z^3 +(3β−2p)z^2 −(pα^2 +3qα+3β^2 −4pβ+p^2 )z −(qα^3 −pα^2 β−3qαβ+pqα−β^3 +2pβ^2 −p^2 β−q^2 )p we want the square and the linear terms to disappear so we set their constants zero to get α and β ⇒ β=((2p)/3); α=−((3q)/(2p))±((√(12p^3 +81q^2 ))/(6p)) this leads to z^3 =((8p^3 )/(27))+((27q^4 )/(2p^3 ))+4q^2 ±((q(√(3(4p^3 +27q^2 )^3 )))/(18p^3 )) Tschirnhaus thought he could solve polynomes of any degree with this method but it′s getting harder to solve because you need a cubic substitution to eliminate 3 constants and so on...

$$\mathrm{found}\:\mathrm{something}\:\mathrm{interesting},\:\mathrm{it}\:\mathrm{was}\:\mathrm{published} \\ $$$$\mathrm{by}\:\mathrm{Tschirnhaus}\:\mathrm{in}\:\mathrm{1683} \\ $$$$\mathrm{we}\:\mathrm{can}\:\mathrm{reduce} \\ $$$${x}^{\mathrm{3}} +{ax}^{\mathrm{2}} +{bx}+{c}=\mathrm{0} \\ $$$$\left(\mathrm{1}\right)\:\mathrm{to} \\ $$$${y}^{\mathrm{3}} +{py}+{q}=\mathrm{0} \\ $$$$\left(\mathrm{2}\right)\:\mathrm{and}\:\mathrm{further}\:\mathrm{to} \\ $$$${z}^{\mathrm{3}} ={t} \\ $$$$ \\ $$$$\left(\mathrm{1}\right)\:\mathrm{is}\:\mathrm{the}\:\mathrm{well}\:\mathrm{known}\:\mathrm{linear}\:\mathrm{substitution} \\ $$$${y}={x}+\frac{{a}}{\mathrm{3}}\:\rightarrow\:{x}={y}−\frac{{a}}{\mathrm{3}} \\ $$$$\Rightarrow\:{y}^{\mathrm{3}} −\frac{{a}^{\mathrm{2}} −\mathrm{3}{b}}{\mathrm{3}}{y}+\frac{\mathrm{2}{a}^{\mathrm{3}} −\mathrm{9}{ab}+\mathrm{27}{c}}{\mathrm{27}}=\mathrm{0} \\ $$$${p}=−\frac{{a}^{\mathrm{2}} −\mathrm{3}{b}}{\mathrm{3}}\:\mathrm{and}\:{q}=\frac{\mathrm{2}{a}^{\mathrm{3}} −\mathrm{9}{ab}+\mathrm{27}{c}}{\mathrm{27}} \\ $$$$\Rightarrow\:{y}^{\mathrm{3}} +{py}+{q}=\mathrm{0} \\ $$$$ \\ $$$$\left(\mathrm{2}\right)\:\mathrm{quadratic}\:\mathrm{substitution} \\ $$$${z}={y}^{\mathrm{2}} +\alpha{y}+\beta\:\rightarrow\:{y}^{\mathrm{2}} +\alpha{y}+\left(\beta−{z}\right)=\mathrm{0} \\ $$$$\mathrm{we}\:\mathrm{could}\:\mathrm{solve}\:\mathrm{this}\:\mathrm{for}\:{y}\:\mathrm{and}\:\mathrm{then}\:\mathrm{plug}\:\mathrm{in} \\ $$$$\mathrm{above}...\:\left(\mathrm{Tschirnhaus}\:\mathrm{did}\right)\:\mathrm{but}\:\mathrm{there}'\mathrm{s}\:\mathrm{an} \\ $$$$\mathrm{easier}\:\mathrm{way}:\:\mathrm{we}\:\mathrm{calculate}\:\mathrm{the}\:\mathrm{determinant}\:\mathrm{of} \\ $$$$\mathrm{the}\:\mathrm{Sylvester}\:\mathrm{Matrix} \\ $$$$\mathrm{we}\:\mathrm{have} \\ $$$$\left({a}\right)\:\mathrm{1}{y}^{\mathrm{3}} +\mathrm{0}{y}^{\mathrm{2}} +{py}+{q}=\mathrm{0} \\ $$$$\left({b}\right)\:\mathrm{0}{y}^{\mathrm{3}} +{y}^{\mathrm{2}} +\alpha{y}+\left(\beta−{z}\right)=\mathrm{0} \\ $$$$\mathrm{the}\:\mathrm{matrix}\:\mathrm{is} \\ $$$$\begin{bmatrix}{\mathrm{1}}&{\mathrm{0}}&{{p}}&{{q}}&{\mathrm{0}}\\{\mathrm{0}}&{\mathrm{1}}&{\mathrm{0}}&{{p}}&{{q}}\\{\mathrm{0}}&{\mathrm{1}}&{\alpha}&{\beta−{z}}&{\mathrm{0}}\\{\mathrm{0}}&{\mathrm{0}}&{\mathrm{1}}&{\alpha}&{\beta−{z}}\\{\mathrm{1}}&{\alpha}&{\beta−{z}}&{\mathrm{0}}&{\mathrm{0}}\end{bmatrix} \\ $$$$\mathrm{the}\:\mathrm{determinant}\:\mathrm{is} \\ $$$$−{z}^{\mathrm{3}} \\ $$$$\:\:+\left(\mathrm{3}\beta−\mathrm{2}{p}\right){z}^{\mathrm{2}} \\ $$$$\:\:−\left({p}\alpha^{\mathrm{2}} +\mathrm{3}{q}\alpha+\mathrm{3}\beta^{\mathrm{2}} −\mathrm{4}{p}\beta+{p}^{\mathrm{2}} \right){z} \\ $$$$\:\:−\left({q}\alpha^{\mathrm{3}} −{p}\alpha^{\mathrm{2}} \beta−\mathrm{3}{q}\alpha\beta+{pq}\alpha−\beta^{\mathrm{3}} +\mathrm{2}{p}\beta^{\mathrm{2}} −{p}^{\mathrm{2}} \beta−{q}^{\mathrm{2}} \right){p} \\ $$$$\mathrm{we}\:\mathrm{want}\:\mathrm{the}\:\mathrm{square}\:\mathrm{and}\:\mathrm{the}\:\mathrm{linear}\:\mathrm{terms} \\ $$$$\mathrm{to}\:\mathrm{disappear}\:\mathrm{so}\:\mathrm{we}\:\mathrm{set}\:\mathrm{their}\:\mathrm{constants}\:\mathrm{zero} \\ $$$$\mathrm{to}\:\mathrm{get}\:\alpha\:\mathrm{and}\:\beta \\ $$$$\Rightarrow\:\beta=\frac{\mathrm{2}{p}}{\mathrm{3}};\:\alpha=−\frac{\mathrm{3}{q}}{\mathrm{2}{p}}\pm\frac{\sqrt{\mathrm{12}{p}^{\mathrm{3}} +\mathrm{81}{q}^{\mathrm{2}} }}{\mathrm{6}{p}} \\ $$$$\mathrm{this}\:\mathrm{leads}\:\mathrm{to} \\ $$$${z}^{\mathrm{3}} =\frac{\mathrm{8}{p}^{\mathrm{3}} }{\mathrm{27}}+\frac{\mathrm{27}{q}^{\mathrm{4}} }{\mathrm{2}{p}^{\mathrm{3}} }+\mathrm{4}{q}^{\mathrm{2}} \pm\frac{{q}\sqrt{\mathrm{3}\left(\mathrm{4}{p}^{\mathrm{3}} +\mathrm{27}{q}^{\mathrm{2}} \right)^{\mathrm{3}} }}{\mathrm{18}{p}^{\mathrm{3}} } \\ $$$$\mathrm{Tschirnhaus}\:\mathrm{thought}\:\mathrm{he}\:\mathrm{could}\:\mathrm{solve}\:\mathrm{polynomes} \\ $$$$\mathrm{of}\:\mathrm{any}\:\mathrm{degree}\:\mathrm{with}\:\mathrm{this}\:\mathrm{method}\:\mathrm{but}\:\mathrm{it}'\mathrm{s}\:\mathrm{getting} \\ $$$$\mathrm{harder}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{because}\:\mathrm{you}\:\mathrm{need}\:\mathrm{a}\:\mathrm{cubic} \\ $$$$\mathrm{substitution}\:\mathrm{to}\:\mathrm{eliminate}\:\mathrm{3}\:\mathrm{constants}\:\mathrm{and} \\ $$$$\mathrm{so}\:\mathrm{on}... \\ $$

Pg 1559 Pg 1560 Pg 1561 Pg 1562 Pg 1563 Pg 1564 Pg 1565 Pg 1566 Pg 1567 Pg 1568

Contact: [email protected]