
AllQuestion and Answers: Page 1562
Question Number 55104 Answers: 0 Comments: 3
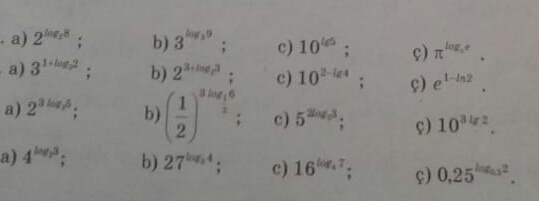
Question Number 55100 Answers: 1 Comments: 5
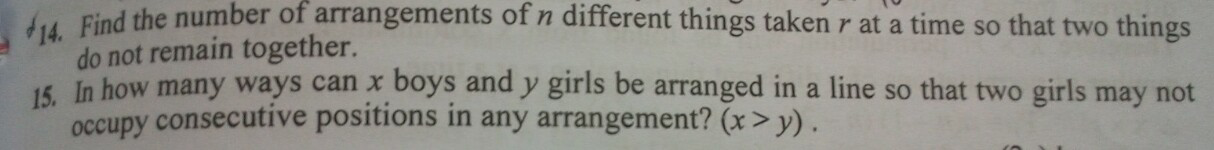
Question Number 55099 Answers: 1 Comments: 0
Question Number 55089 Answers: 0 Comments: 1
Question Number 55088 Answers: 0 Comments: 0
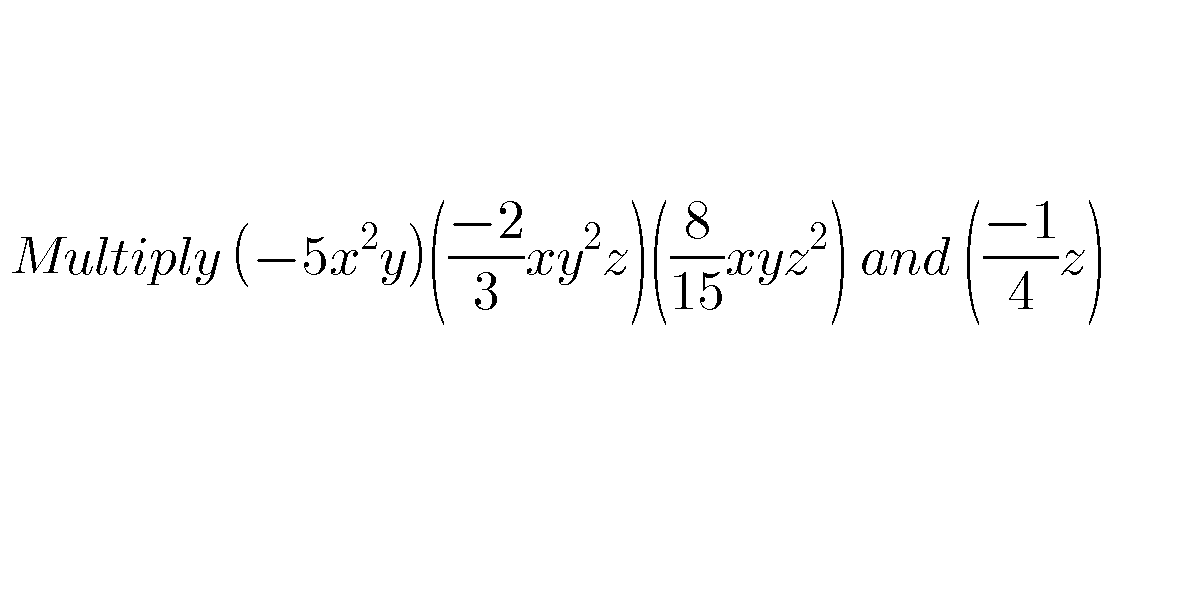
Question Number 55087 Answers: 0 Comments: 1
Question Number 55094 Answers: 2 Comments: 2
Question Number 55083 Answers: 0 Comments: 0

Question Number 55076 Answers: 1 Comments: 0
Question Number 55070 Answers: 0 Comments: 1
Question Number 55069 Answers: 1 Comments: 3
Question Number 55068 Answers: 0 Comments: 0
Question Number 55067 Answers: 0 Comments: 0
Question Number 55066 Answers: 0 Comments: 0
Question Number 55059 Answers: 0 Comments: 0
Question Number 55058 Answers: 0 Comments: 0
Question Number 55057 Answers: 0 Comments: 0
Question Number 55055 Answers: 1 Comments: 0

Question Number 55054 Answers: 0 Comments: 0

Question Number 55052 Answers: 0 Comments: 3

Question Number 55051 Answers: 0 Comments: 1
Question Number 55454 Answers: 0 Comments: 3
Question Number 55044 Answers: 1 Comments: 2
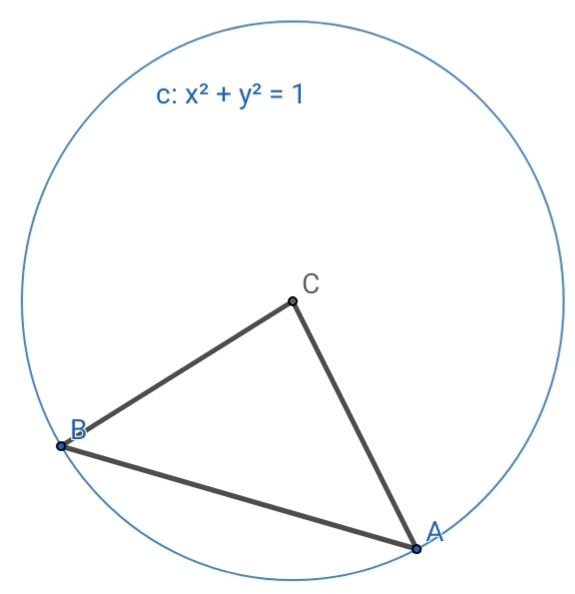
Question Number 55039 Answers: 1 Comments: 3
Question Number 55030 Answers: 1 Comments: 5
Question Number 55006 Answers: 1 Comments: 0

Pg 1557 Pg 1558 Pg 1559 Pg 1560 Pg 1561 Pg 1562 Pg 1563 Pg 1564 Pg 1565 Pg 1566
