
AllQuestion and Answers: Page 1561
Question Number 54825 Answers: 1 Comments: 0

Question Number 54808 Answers: 1 Comments: 2
Question Number 54797 Answers: 1 Comments: 0
Question Number 54821 Answers: 0 Comments: 1
Question Number 54790 Answers: 3 Comments: 2
Question Number 54788 Answers: 2 Comments: 1
Question Number 54787 Answers: 0 Comments: 0
Question Number 54786 Answers: 0 Comments: 5
Question Number 54777 Answers: 0 Comments: 1
Question Number 54775 Answers: 0 Comments: 2
Question Number 54770 Answers: 0 Comments: 0
Question Number 54767 Answers: 1 Comments: 1
Question Number 54765 Answers: 1 Comments: 0

Question Number 54756 Answers: 1 Comments: 0
Question Number 54755 Answers: 1 Comments: 0
Question Number 54745 Answers: 0 Comments: 0
Question Number 54741 Answers: 1 Comments: 1
Question Number 54740 Answers: 3 Comments: 0
Question Number 54737 Answers: 0 Comments: 0

Question Number 54730 Answers: 0 Comments: 3
Question Number 54716 Answers: 0 Comments: 6
Question Number 54721 Answers: 0 Comments: 0
Question Number 54701 Answers: 2 Comments: 0
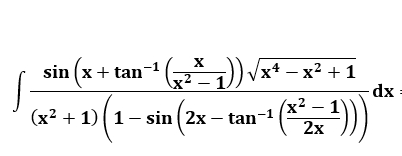
Question Number 54700 Answers: 1 Comments: 1
Question Number 54699 Answers: 2 Comments: 3
Question Number 54698 Answers: 2 Comments: 0
Pg 1556 Pg 1557 Pg 1558 Pg 1559 Pg 1560 Pg 1561 Pg 1562 Pg 1563 Pg 1564 Pg 1565
