Question and Answers Forum

Prove that: (a) If ∣z_1 + z_2 ∣ = ∣z_1 − z_2 ∣, the difference of the arguements of z_1 and z_2 is (π/2) (b) If arg{((z_1 + z_2 )/(z_1 − z_2 ))} = (π/2) , then ∣z_1 ∣ = ∣z_2 ∣

Question Number 51163 Answers: 0 Comments: 0

Question Number 51156 Answers: 2 Comments: 0

Show that the equation of tangent to the ellipse (x^2 /a^2 )+(y^2 /b^2 )=1 at the end of lactus rectum which lie in the 1^(st) quadrant is xe+y−a=0 ∗merry X−mas and happy new year∗

$${Show}\:{that}\:{the}\:{equation} \\ $$$${of}\:{tangent}\:{to}\:{the}\:{ellipse} \\ $$$$\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1}\:{at}\:{the}\:{end}\:{of} \\ $$$${lactus}\:{rectum}\:{which} \\ $$$${lie}\:{in}\:{the}\:\mathrm{1}^{{st}} {quadrant}\:{is} \\ $$$${xe}+{y}−{a}=\mathrm{0} \\ $$$$ \\ $$$$\ast{merry}\:{X}−{mas}\:{and}\:{happy}\:{new}\:{year}\ast \\ $$

Question Number 51153 Answers: 3 Comments: 1

Question Number 51214 Answers: 3 Comments: 0

1.lim_(x→−(i/2)) (((z−i)^2 )/((2z−i)(3−z))) 2.lim_(x→e^((πi)/4) ) ((2z^2 )/(z^3 −z−1)) 3.lim_(x→2i) ((2z^2 +8)/((√z^4 )−^3 (√(64)))) 4.lim_(x→0) ((cos 4z−1)/(z sin z))

$$\mathrm{1}.\underset{{x}\rightarrow−\frac{\mathrm{i}}{\mathrm{2}}} {\mathrm{lim}}\:\frac{\left({z}−{i}\right)^{\mathrm{2}} }{\left(\mathrm{2}{z}−{i}\right)\left(\mathrm{3}−{z}\right)} \\ $$$$\mathrm{2}.\underset{{x}\rightarrow{e}^{\frac{\pi{i}}{\mathrm{4}}} } {\mathrm{lim}}\:\frac{\mathrm{2}{z}^{\mathrm{2}} }{{z}^{\mathrm{3}} −{z}−\mathrm{1}} \\ $$$$\mathrm{3}.\underset{{x}\rightarrow\mathrm{2}{i}} {\mathrm{lim}}\:\frac{\mathrm{2}{z}^{\mathrm{2}} +\mathrm{8}}{\sqrt{{z}^{\mathrm{4}} }−^{\mathrm{3}} \sqrt{\mathrm{64}}} \\ $$$$\mathrm{4}.\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{cos}\:\mathrm{4}{z}−\mathrm{1}}{{z}\:\mathrm{sin}\:{z}} \\ $$$$ \\ $$

Question Number 51151 Answers: 1 Comments: 0

Find the equation of tangent to the ellipse x^2 +4y^2 =4 which are perpendicular to the line 2x−3y=1 ∗merry X−mas and happy new year∗

$${Find}\:{the}\:{equation}\:{of} \\ $$$${tangent}\:{to}\:{the}\:\:{ellipse} \\ $$$${x}^{\mathrm{2}} +\mathrm{4}{y}^{\mathrm{2}} =\mathrm{4}\:{which}\:{are} \\ $$$${perpendicular}\:{to}\:{the}\: \\ $$$${line}\:\mathrm{2}{x}−\mathrm{3}{y}=\mathrm{1} \\ $$$$ \\ $$$$\ast{merry}\:{X}−{mas}\:{and}\:{happy}\:{new}\:{year}\ast \\ $$

Question Number 51150 Answers: 2 Comments: 0

from left hand sides prove that ((sinαsin β)/(cos α+cos β))=((2tan(α/2) tan (β/2))/(1−tan^2 (α/2)tan^2 (β/2)))

$${from}\:{left}\:{hand}\:{sides} \\ $$$${prove}\:{that} \\ $$$$\frac{{sin}\alpha\mathrm{sin}\:\beta}{\mathrm{cos}\:\alpha+\mathrm{cos}\:\beta}=\frac{\mathrm{2tan}\frac{\alpha}{\mathrm{2}}\:\mathrm{tan}\:\frac{\beta}{\mathrm{2}}}{\mathrm{1}−\mathrm{tan}\:^{\mathrm{2}} \frac{\alpha}{\mathrm{2}}\mathrm{tan}^{\mathrm{2}} \:\frac{\beta}{\mathrm{2}}} \\ $$

Question Number 51148 Answers: 1 Comments: 0

Two hot cubes are at same temperature and both are cooled by forced convetion the cube are made from the same material but one has side of L metre and other one 2L metre. which cube is at quicker rate of cooling

$${Two}\:{hot}\:{cubes}\:{are}\:\:{at}\:{same}\: \\ $$$${temperature}\:{and} \\ $$$${both}\:{are}\:{cooled}\:{by}\:{forced}\: \\ $$$${convetion}\:{the}\:{cube}\:{are}\:{made} \\ $$$${from}\:{the}\:{same}\:{material} \\ $$$${but}\:{one}\:{has}\:{side}\:{of}\:{L}\:{metre} \\ $$$${and}\:{other}\:{one}\:\mathrm{2}{L}\:{metre}. \\ $$$${which}\:{cube}\:{is}\:{at}\:{quicker}\: \\ $$$${rate}\:{of}\:{cooling} \\ $$$$ \\ $$

Question Number 51141 Answers: 1 Comments: 0

Question Number 51134 Answers: 1 Comments: 1

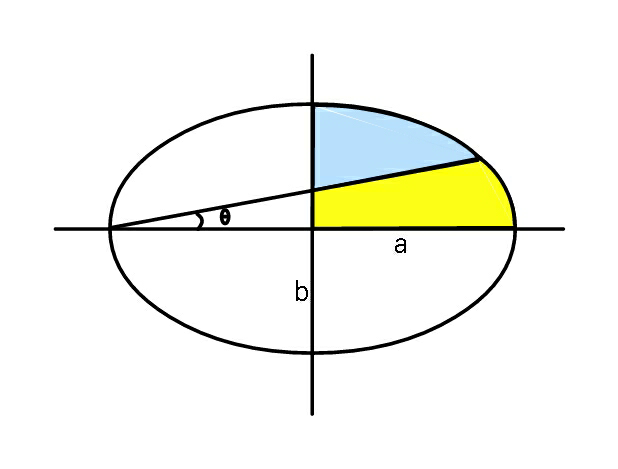
Question Number 51122 Answers: 1 Comments: 1

∫ (dx/(tgx−(√(tgx))))=?

$$\int\:\:\:\:\frac{\boldsymbol{\mathrm{dx}}}{\boldsymbol{\mathrm{tgx}}−\sqrt{\boldsymbol{\mathrm{tgx}}}}=? \\ $$

Question Number 51107 Answers: 2 Comments: 1

A ball is bouncing down a flight of stairs.The coefficiate of restitution is e.The height of each step d and the ball descends one step at each bounce. After each bounce it rebounds to heigt h above the next lower step.The height h is/ large enough compare with width of a step that the empacts are effectively head on.show that h=(d/(1−e^2 ))

$${A}\:{ball}\:{is}\:{bouncing}\:{down} \\ $$$${a}\:{flight}\:{of}\:{stairs}.{The}\: \\ $$$${coefficiate}\:{of}\:{restitution} \\ $$$${is}\:{e}.{The}\:{height}\:{of}\:{each}\:{step} \\ $$$${d}\:{and}\:{the}\:{ball}\:{descends} \\ $$$${one}\:{step}\:{at}\:{each}\:{bounce}. \\ $$$${After}\:{each}\:{bounce}\:{it}\:{rebounds} \\ $$$${to}\:{heigt}\:\:{h}\:{above}\:{the}\:{next} \\ $$$${lower}\:{step}.{The}\:{height}\:{h}\:{is}/ \\ $$$${large}\:{enough}\:{compare}\:{with} \\ $$$${width}\:{of}\:{a}\:{step}\:{that} \\ $$$${the}\:{empacts}\:{are}\:{effectively}\: \\ $$$${head}\:{on}.{show}\:{that} \\ $$$${h}=\frac{{d}}{\mathrm{1}−{e}^{\mathrm{2}} } \\ $$$$ \\ $$

Question Number 51109 Answers: 0 Comments: 1

Question Number 51098 Answers: 1 Comments: 0

Two similar spherical bodies of radius R and 2R are initially are at same temperature.if they are kept to cool under the same condition.show qualitatively which of the two spherical body will cool faster.

Question Number 51095 Answers: 0 Comments: 5

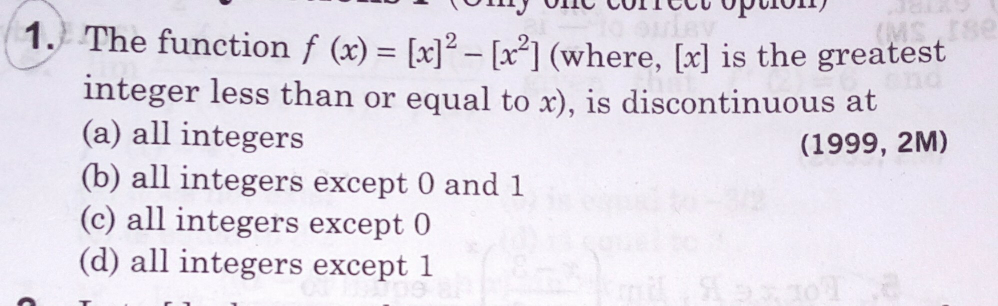
Question Number 51088 Answers: 2 Comments: 1

Question Number 51077 Answers: 0 Comments: 0

$$ \\ $$$$ \\ $$$$ \\ $$

Question Number 51075 Answers: 0 Comments: 0

$$ \\ $$

Question Number 51115 Answers: 0 Comments: 0

Question Number 51069 Answers: 3 Comments: 0

If sinA+cos2A =(1/2) and cosA+sin2A=(1/3) , then find the value of sin3A.

$${If}\:\mathrm{sin}{A}+\mathrm{cos2}{A}\:=\frac{\mathrm{1}}{\mathrm{2}}\:{and} \\ $$$$\mathrm{cos}{A}+\mathrm{sin2}{A}=\frac{\mathrm{1}}{\mathrm{3}}\:,\:{then}\:{find}\:{the}\:{value} \\ $$$${of}\:\mathrm{sin3}{A}. \\ $$

Pg 1553 Pg 1554 Pg 1555 Pg 1556 Pg 1557 Pg 1558 Pg 1559 Pg 1560 Pg 1561 Pg 1562

Contact: info@tinkutara.com