
AllQuestion and Answers: Page 1557
Question Number 51316 Answers: 0 Comments: 2

Question Number 51314 Answers: 0 Comments: 1

Question Number 51312 Answers: 0 Comments: 1

Question Number 51307 Answers: 0 Comments: 3
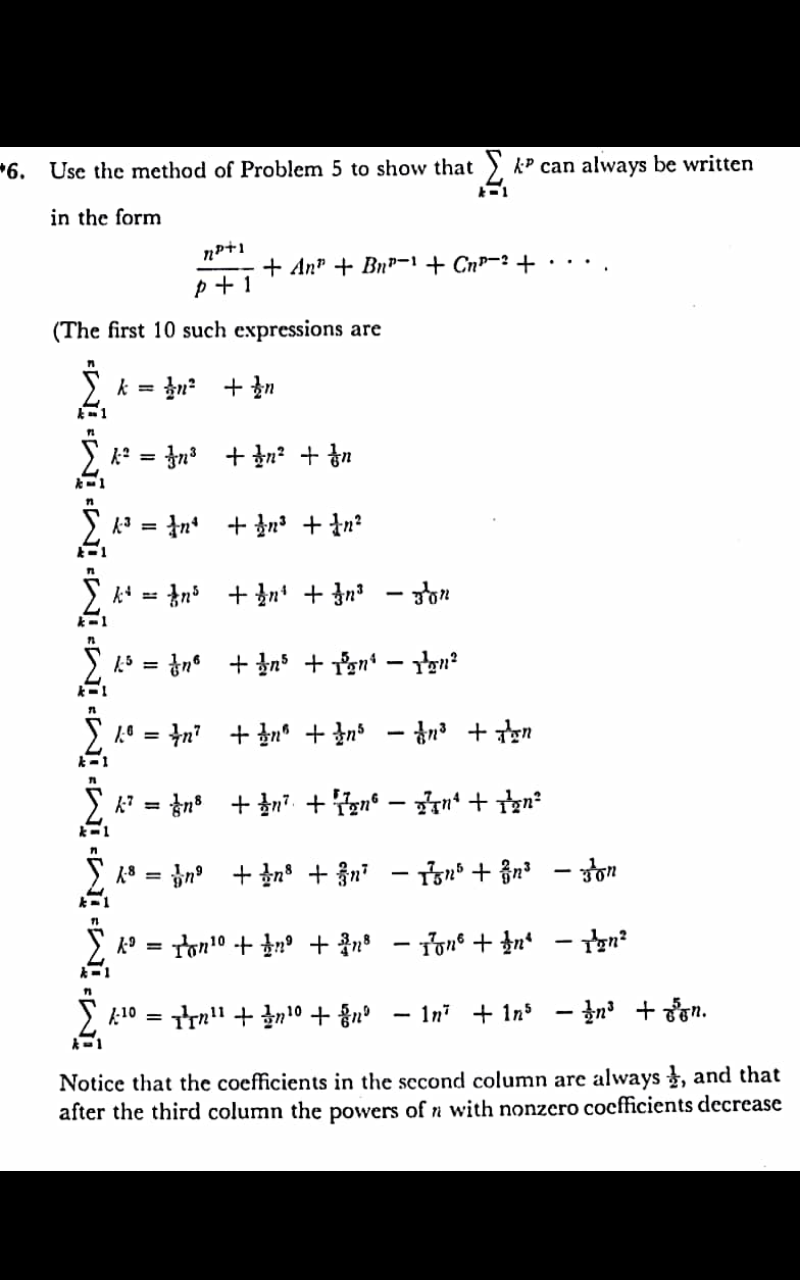
Question Number 51299 Answers: 0 Comments: 4
Question Number 51289 Answers: 1 Comments: 5
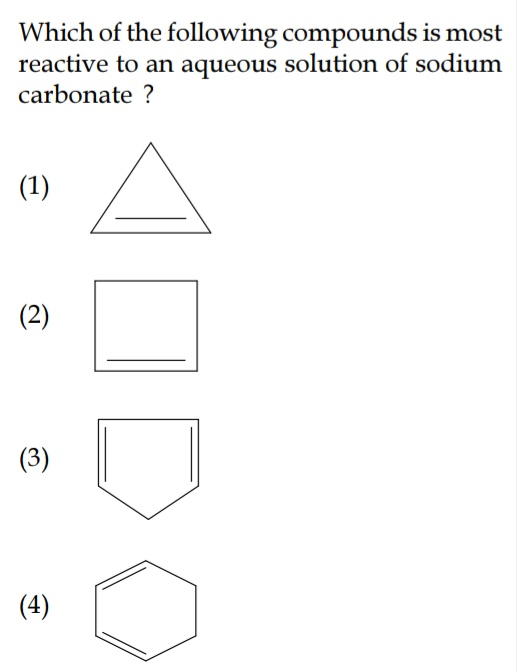
Question Number 51287 Answers: 1 Comments: 0

Question Number 51286 Answers: 1 Comments: 0

Question Number 51284 Answers: 1 Comments: 1
Question Number 51279 Answers: 1 Comments: 1
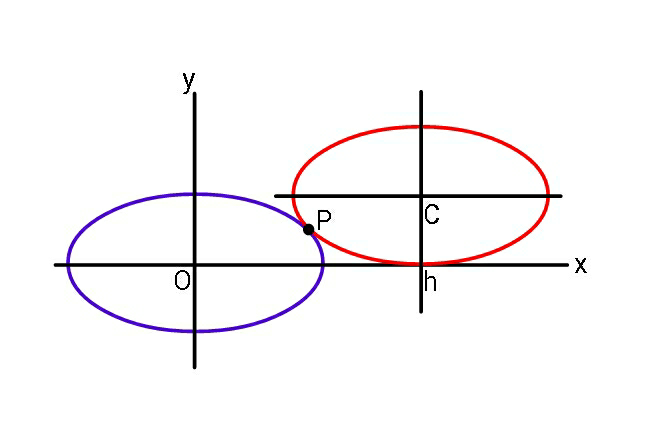
Question Number 51271 Answers: 1 Comments: 0
Question Number 51269 Answers: 1 Comments: 0
Question Number 51263 Answers: 1 Comments: 0
Question Number 51250 Answers: 1 Comments: 0
Question Number 51248 Answers: 1 Comments: 0
Question Number 51245 Answers: 2 Comments: 0

Question Number 51228 Answers: 1 Comments: 1

Question Number 51227 Answers: 1 Comments: 4
Question Number 51220 Answers: 1 Comments: 1
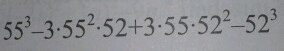
Question Number 51218 Answers: 0 Comments: 0
Question Number 51217 Answers: 0 Comments: 0
Question Number 51216 Answers: 1 Comments: 0
Question Number 51215 Answers: 1 Comments: 0
$$\int_{\mathrm{0}} ^{\pi} {e}^{\left(\mathrm{1}+{i}\right){x}} {dx}=... \\ $$
Question Number 51199 Answers: 0 Comments: 0

Question Number 51236 Answers: 2 Comments: 0
Question Number 51235 Answers: 2 Comments: 0
Pg 1552 Pg 1553 Pg 1554 Pg 1555 Pg 1556 Pg 1557 Pg 1558 Pg 1559 Pg 1560 Pg 1561
