Question and Answers Forum

AllQuestion and Answers: Page 1554

Question Number 51600 Answers: 1 Comments: 1

solve (sinθ)Z^2 −i(cosθ)Z+(1/4) sinθ=0

$$\mathrm{solve} \\ $$$$\left(\mathrm{sin}\theta\right)\mathrm{Z}^{\mathrm{2}} −\mathrm{i}\left(\mathrm{cos}\theta\right)\mathrm{Z}+\frac{\mathrm{1}}{\mathrm{4}}\:\mathrm{sin}\theta=\mathrm{0} \\ $$

Question Number 51594 Answers: 0 Comments: 0

Question Number 51592 Answers: 0 Comments: 4

Question Number 51590 Answers: 2 Comments: 1

The line y=mx+c touches ellipse (x^2 /a^2 )+(y^2 /b^2 )=1 prove that the foot of perpendicular from focus into this line lie on auxillary circle x^2 +y^2 =a^2

$${The}\:{line}\:{y}={mx}+{c}\:{touches} \\ $$$${ellipse}\:\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$${prove}\:{that}\:{the}\:{foot}\:{of}\: \\ $$$${perpendicular}\:{from} \\ $$$${focus}\:{into}\:{this}\:{line}\:{lie}\:{on} \\ $$$${auxillary}\:{circle}\: \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} ={a}^{\mathrm{2}} \\ $$

Question Number 51588 Answers: 1 Comments: 0

The tangent at P to an ellipse meets directrix at Q prove that the line joining the corresponding focus to P and Q are perpendicular

$${The}\:{tangent}\:{at}\:{P}\:\:{to}\:{an}\:{ellipse} \\ $$$${meets}\:{directrix}\:{at}\:{Q} \\ $$$${prove}\:{that}\:{the}\:{line} \\ $$$${joining}\:{the}\:{corresponding} \\ $$$${focus}\:{to}\:{P}\:{and}\:{Q}\:{are} \\ $$$${perpendicular} \\ $$

Question Number 51605 Answers: 0 Comments: 0

Question Number 51571 Answers: 1 Comments: 0

If α − jβ = (1/(a − jb)) , where α, β, a, b are real, express b in terms of α, β Answer: ((− β)/(α^2 + β^2 − 2α + 1))

$$\mathrm{If}\:\:\:\alpha\:−\:\mathrm{j}\beta\:\:=\:\:\frac{\mathrm{1}}{\mathrm{a}\:−\:\mathrm{jb}}\:\:,\:\:\:\:\:\:\mathrm{where}\:\:\:\alpha,\:\beta,\:\mathrm{a},\:\mathrm{b}\:\:\mathrm{are}\:\mathrm{real},\:\mathrm{express}\:\:\mathrm{b}\:\:\mathrm{in}\:\mathrm{terms} \\ $$$$\mathrm{of}\:\:\alpha,\:\beta\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{Answer}:\:\:\:\:\:\:\:\:\:\:\frac{−\:\beta}{\alpha^{\mathrm{2}} \:+\:\beta^{\mathrm{2}} \:−\:\mathrm{2}\alpha\:+\:\mathrm{1}} \\ $$

Question Number 51558 Answers: 1 Comments: 3

Question Number 51552 Answers: 0 Comments: 1

calculate ∫_0 ^(+∞) ((arctan(1+x^2 ))/(x^2 +4))dx

$${calculate}\:\int_{\mathrm{0}} ^{+\infty} \:\:\frac{{arctan}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{{x}^{\mathrm{2}} \:+\mathrm{4}}{dx} \\ $$

Question Number 51551 Answers: 2 Comments: 2

find f(λ) = ∫_0 ^(π/4) (√(1+λtant))dt with λ>0 also calculate ∫_0 ^(π/4) ((tant)/(√(1+λtant)))dt.

$${find}\:{f}\left(\lambda\right)\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \sqrt{\mathrm{1}+\lambda{tant}}{dt}\:\:\:{with}\:\lambda>\mathrm{0} \\ $$$${also}\:{calculate}\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\frac{{tant}}{\sqrt{\mathrm{1}+\lambda{tant}}}{dt}. \\ $$

Question Number 51550 Answers: 1 Comments: 2

find ∫_0 ^1 (√(1+x^4 ))dx

$${find}\:\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\mathrm{1}+{x}^{\mathrm{4}} }{dx} \\ $$

Question Number 51549 Answers: 0 Comments: 0

A and B are two points from the plan (P) with AB=4 define and draw the locus of points M ∈(P) wich verify MA +MB =8 .

$${A}\:{and}\:{B}\:{are}\:{two}\:{points}\:{from}\:{the}\:{plan}\:\left({P}\right)\:{with}\:{AB}=\mathrm{4}\:{define}\:{and}\:{draw} \\ $$$${the}\:{locus}\:{of}\:{points}\:{M}\:\in\left({P}\right)\:{wich}\:{verify}\:\:\:{MA}\:+{MB}\:=\mathrm{8}\:. \\ $$

Question Number 51539 Answers: 2 Comments: 1

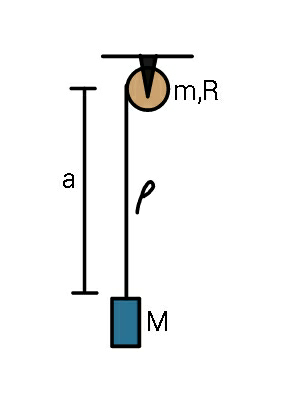
Question Number 51535 Answers: 1 Comments: 1

Question Number 51526 Answers: 1 Comments: 1

Question Number 51510 Answers: 1 Comments: 0

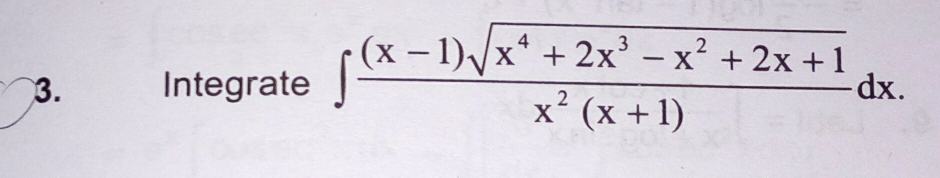
Question Number 51508 Answers: 0 Comments: 0

A man walking due to west along a level road observes a school in a direction N 72° E. After walking 1500 yards, he observes it in a direction N 67° E. How far is the school from the road.

$$\mathrm{A}\:\mathrm{man}\:\mathrm{walking}\:\mathrm{due}\:\mathrm{to}\:\mathrm{west}\:\mathrm{along}\:\mathrm{a}\:\mathrm{level}\:\mathrm{road}\:\mathrm{observes}\:\mathrm{a}\:\mathrm{school}\:\mathrm{in}\:\mathrm{a}\:\mathrm{direction}\:\mathrm{N}\:\mathrm{72}°\:\mathrm{E}.\:\mathrm{After}\:\mathrm{walking}\:\mathrm{1500}\:\mathrm{yards},\: \\ $$$$\mathrm{he}\:\mathrm{observes}\:\mathrm{it}\:\mathrm{in}\:\mathrm{a}\:\mathrm{direction}\:\mathrm{N}\:\mathrm{67}°\:\mathrm{E}.\:\mathrm{How}\:\mathrm{far}\:\mathrm{is}\:\mathrm{the}\:\mathrm{school}\:\mathrm{from}\:\mathrm{the}\:\mathrm{road}. \\ $$

Question Number 51502 Answers: 0 Comments: 1

Question Number 51501 Answers: 1 Comments: 0

Question Number 51507 Answers: 0 Comments: 0

^• 739 is a prime number and its reversed number 937 is also prime. Determine 4-digit prime numbers whose reversed be also prime. ^• If number of such primes is a function of number of digits, determine that the function is increasing or not.

$$\:^{\bullet} \mathrm{739}\:{is}\:{a}\:\:{prime}\:{number}\:{and} \\ $$$${its}\:{reversed}\:{number}\:\mathrm{937}\:{is}\:{also} \\ $$$${prime}. \\ $$$${Determine}\:\mathrm{4}-{digit}\:{prime}\:{numbers} \\ $$$${whose}\:{reversed}\:{be}\:{also}\:{prime}. \\ $$$$\:^{\bullet} {If}\:{number}\:{of}\:{such}\:{primes}\:{is}\:{a} \\ $$$${function}\:{of}\:{number}\:{of}\:{digits}, \\ $$$${determine}\:{that}\:{the}\:{function}\:{is} \\ $$$${increasing}\:{or}\:{not}. \\ $$

Question Number 51494 Answers: 0 Comments: 2

Solve: (t^2 + 1) (dp/dt) = p^t

$$\mathrm{Solve}:\:\:\:\:\:\:\:\:\left(\mathrm{t}^{\mathrm{2}} \:+\:\mathrm{1}\right)\:\frac{\mathrm{dp}}{\mathrm{dt}}\:\:=\:\:\mathrm{p}^{\mathrm{t}} \\ $$

Question Number 51492 Answers: 1 Comments: 0

For ellipse 16x^2 +4y^2 +96x−8y−84=0 find i)centre ii)verteces iii)focus iv)directrix v)length of major and minor axis vi)ecentricity vii)graph the ellipse

$${For}\:{ellipse}\: \\ $$$$\mathrm{16}{x}^{\mathrm{2}} +\mathrm{4}{y}^{\mathrm{2}} +\mathrm{96}{x}−\mathrm{8}{y}−\mathrm{84}=\mathrm{0} \\ $$$${find} \\ $$$$\left.{i}\right){centre} \\ $$$$\left.{ii}\right){verteces} \\ $$$$\left.{iii}\right){focus} \\ $$$$\left.{iv}\right){directrix} \\ $$$$\left.{v}\right){length}\:{of}\:{major}\: \\ $$$${and}\:{minor}\:{axis} \\ $$$$\left.{vi}\right){ecentricity} \\ $$$$\left.{vii}\right){graph}\:{the}\:{ellipse} \\ $$

Question Number 51489 Answers: 1 Comments: 0

Given that y=mx+c is equation of tangent to the ellipse (x^2 /a^(2 ) )+(y^2 /b^2 )=1 find coordinate of point of contact.

$${Given}\:{that}\:{y}={mx}+{c} \\ $$$${is}\:{equation}\:{of}\:\:{tangent} \\ $$$${to}\:{the}\:{ellipse}\:\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}\:} }+\frac{{y}^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$${find}\:{coordinate}\:{of}\: \\ $$$${point}\:{of}\:{contact}. \\ $$

Question Number 51485 Answers: 0 Comments: 1

Question Number 51520 Answers: 1 Comments: 1

Question Number 51448 Answers: 0 Comments: 3

Pg 1549 Pg 1550 Pg 1551 Pg 1552 Pg 1553 Pg 1554 Pg 1555 Pg 1556 Pg 1557 Pg 1558

Contact: info@tinkutara.com